Strona główna > Matematyka > Geometria płaszczyzny > Twierdzenie Pitagorasa
a2+b2=c2
Znając długości pary boków trójkąta prostokątnego można wyznaczyć trzeci bok z następujących wzorów:
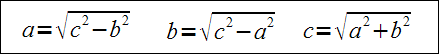
Na poniższym rysunku pokazano geometryczną interpretację twierdzenia Pitagorasa: suma pól kwadratów zbudowanych na przyprostokątnych jest równa polu kwadratu zbudowanego na przeciwprostokątnej.


Na powyższym rysunku po lewej stronie został pokazany trójkąt prostokątny. Wykorzystując cztery takie trójkąty zbudujmy figurę pokazaną po prawej stronie. Pole kwadratu KLMN jest równe (a+b)2. Jednocześnie jest ono równe sumie pól wewnętrznego kwadratu GHIJ i czterech trójkątów prostokątnych zaznaczonych na rysunku żółtym kolorem. Możemy zatem zapisać to następująco:
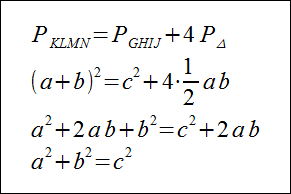
Rozwiązanie
Do rozwiązania zadania stosujemy wzór:
c2=a2+b2
b2=c2-a2
b2=52-32
b2=25-9
b2=16
b=4
2012-06-16 18:49:20 Amanda18 napisał(a):
Przydatne :*
2012-06-18 00:44:52 Zulik napisał(a):
Jutro mam klasówkę z tego ale tę podstawę umiem , nie wiem czego mam się tam spodziewać ale miejmy nadzieję, że mi się uda :) Pozdrawiam !
2013-03-05 19:22:10 oli23 napisał(a):
a o co chodzi w Twierdzeniu pitagorasa w układzie współrzędnych?? bo nie rozumiem tego za bardzo proszę o pomoc
Twierdzenie Pitagorasa
W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.a2+b2=c2
Znając długości pary boków trójkąta prostokątnego można wyznaczyć trzeci bok z następujących wzorów:
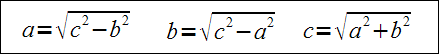
Na poniższym rysunku pokazano geometryczną interpretację twierdzenia Pitagorasa: suma pól kwadratów zbudowanych na przyprostokątnych jest równa polu kwadratu zbudowanego na przeciwprostokątnej.

Dla ciekawskich - dowód twierdzenia Pitagorasa
Twierdzenie to doczekało się bardzo wielu różnych dowodów. Szacuje się, że na dzień dzisiejszy jest ich ponad 100! Można tu wymienić dowody: osiem dowodów Euklidesa,dowód Nassir-ed-Dina (1594r.), dowody Hoffmana (1821r.), dowód Tempelhoffa (1769 r.), dowód Wernera (1855r.) i wiele innych. Poniżej przedstawiamy jeden z wielu dowodów tego twierdzenia:
Na powyższym rysunku po lewej stronie został pokazany trójkąt prostokątny. Wykorzystując cztery takie trójkąty zbudujmy figurę pokazaną po prawej stronie. Pole kwadratu KLMN jest równe (a+b)2. Jednocześnie jest ono równe sumie pól wewnętrznego kwadratu GHIJ i czterech trójkątów prostokątnych zaznaczonych na rysunku żółtym kolorem. Możemy zatem zapisać to następująco:
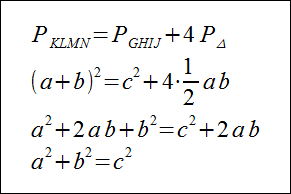
Twierdzenie Pitagorasa - zadanie
Dany jest trójkąt prostokątny o przeciwprostokątnej równej 5 i jednej z przyprostokątnych równej 3. Oblicz długość drugiej przyprostokątnej.Rozwiązanie
Do rozwiązania zadania stosujemy wzór:
c2=a2+b2
b2=c2-a2
b2=52-32
b2=25-9
b2=16
b=4
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (3)
2012-06-16 18:49:20 Amanda18 napisał(a):
Przydatne :*
2012-06-18 00:44:52 Zulik napisał(a):
Jutro mam klasówkę z tego ale tę podstawę umiem , nie wiem czego mam się tam spodziewać ale miejmy nadzieję, że mi się uda :) Pozdrawiam !
2013-03-05 19:22:10 oli23 napisał(a):
a o co chodzi w Twierdzeniu pitagorasa w układzie współrzędnych?? bo nie rozumiem tego za bardzo proszę o pomoc