Strona główna > Matematyka > Geometria płaszczyzny > Trójkąt 30 60 90



Oblicz pole trójkąta o kątach 30, 60, 90, którego przeciwprostokątna jest równa 4.
Zadanie 1 - rozwiązanie
Korzystamy z wzoru na pole trójkąta 30,60,90.

Stąd otrzymujemy: P=42 * (pierwiastek z 3)/8 = 2 * (pierwiastek z 3)
2012-06-26 22:01:55 Artur napisał(a):
Świetny artykuł. Pomógł ;)
2013-03-25 21:55:32 Matplk napisał(a):
Jak obliczyć 2a i a gdy mamy podaną wysokość ?
2013-03-25 22:16:49 BazyWiedzy.COM napisał(a):
Witaj.
Zakładam, że chodzi Ci o wysokość, która jest jednocześnie jedną z przyprostokątnych. Trzymając się Twoich oznaczeń mamy : przeciwprostokątna 2a, przyprostokątna a, druga przyprostokątna a √3 = h. Jeśli mamy teraz dane h to rozwiązujemy proste równanie i wyznaczamy a:
h=a √3 |:√3
h/√3 = a
Stąd mamy także:
2h/√3 = 2a
Pozdrawiam Marcin
2013-04-09 19:25:54 [email protected] napisał(a):
Może ktoś mi powiedzieć jak udowodnić długości przyprostokątnych jeżeli przeciwprostokątna to a?
2013-04-09 20:12:37 BazyWiedzy.COM napisał(a):
Aby to udowodnić bierzemy trójkąt równoboczny o boku a i rysujemy dwusieczną jednego z kątów 60 stopni. Dzieli ona przeciwległy bok na dwie równe części 0.5 a. Powstają w ten sposób dwa trójkąty 30 60 90. Trzeci bok (h) wyznaczamy z twierdzenia Pitagorasa:

2013-04-09 22:26:42 katia1300 napisał(a):
dziękuję :)
2013-05-21 22:04:44 Zina napisał(a):
Prosze o szybka pomoc.
2234.docx
2015-12-04 18:56:15 janeczka napisał(a):
Moi Drodzy - mnie chodzi o potwierdzenie, że w podręcznikach matematycznych, trójkąt o kątach 90, 30 i 60 stopni miał nazwę "piękny". Zaznaczam miał nazwę, bo obecnie tak się nie nazywa tego trójkąta. Potwierdzenia tej nazwy jest dla mnie ważne. Dziękuję jeśli Państwo odnajdziecie. Na pewno będą to podręczniki dla szkół średnich okresu przedwojennego, czyli przed 1939 rokiem.
2015-12-07 13:22:28 janeczka napisał(a):
Pytanie dotyczy poprzedniego - czyli czy trójkąt prostokątny nosi nazwę "piękny". Dawno, kilkanaście lat wstecz miałam podręcznik z lat przed 1939r. W nim przeczytałam tę nazwę, ale podręcznik nie zachował się. Nazwa była w internecie, a tera jako takiej nie mogę odszukać. jest to bardzo potrzebne do korzystania bezpośrednio z jego własności, bez dodatkowych obliczeń. Dlatego poszukuję potwierdzenia. Dziękuję za pomoc i oczekuję pilnie.
2015-12-08 12:36:54 janeczka napisał(a):
Ślicznie dziękuję, bo dzięki Wam Śzanowni Pastwo mam informację o trójkącie pięknym. Ukłony dla Was.
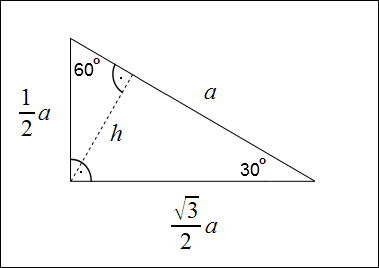
Trójkąt 30 60 90
Na poniższym rysunku przedstawiono trójkąt prostokątny, w którym dwa pozostałe kąty mają miary 30 i 60 stopni.
Pole trójkąta 30 60 90
Wzór na pole trójkąta 30 60 90 wyprowadzamy ze znanego wzoru na pole trójkąta:
Obwód trójkąta 30 60 90

Wysokości trójkąta 30 60 90
Dwie wysokości omawianego trójkąta zawierają się w jego przyprostokątnych. Długość trzeciej wysokości h (poprowadzonej z wierzchołka kąta 90 stopni) obliczymy korzystając z wzoru na pole trójkąta:
Trójkąt 30 60 90 : zadania
Zadanie 1Oblicz pole trójkąta o kątach 30, 60, 90, którego przeciwprostokątna jest równa 4.
Zadanie 1 - rozwiązanie
Korzystamy z wzoru na pole trójkąta 30,60,90.

Stąd otrzymujemy: P=42 * (pierwiastek z 3)/8 = 2 * (pierwiastek z 3)
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (10)
2012-06-26 22:01:55 Artur napisał(a):
Świetny artykuł. Pomógł ;)
2013-03-25 21:55:32 Matplk napisał(a):
Jak obliczyć 2a i a gdy mamy podaną wysokość ?
2013-03-25 22:16:49 BazyWiedzy.COM napisał(a):
Witaj.
Zakładam, że chodzi Ci o wysokość, która jest jednocześnie jedną z przyprostokątnych. Trzymając się Twoich oznaczeń mamy : przeciwprostokątna 2a, przyprostokątna a, druga przyprostokątna a √3 = h. Jeśli mamy teraz dane h to rozwiązujemy proste równanie i wyznaczamy a:
h=a √3 |:√3
h/√3 = a
Stąd mamy także:
2h/√3 = 2a
Pozdrawiam Marcin
2013-04-09 19:25:54 [email protected] napisał(a):
Może ktoś mi powiedzieć jak udowodnić długości przyprostokątnych jeżeli przeciwprostokątna to a?
2013-04-09 20:12:37 BazyWiedzy.COM napisał(a):
Aby to udowodnić bierzemy trójkąt równoboczny o boku a i rysujemy dwusieczną jednego z kątów 60 stopni. Dzieli ona przeciwległy bok na dwie równe części 0.5 a. Powstają w ten sposób dwa trójkąty 30 60 90. Trzeci bok (h) wyznaczamy z twierdzenia Pitagorasa:

2013-04-09 22:26:42 katia1300 napisał(a):
dziękuję :)
2013-05-21 22:04:44 Zina napisał(a):
Prosze o szybka pomoc.
2234.docx
2015-12-04 18:56:15 janeczka napisał(a):
Moi Drodzy - mnie chodzi o potwierdzenie, że w podręcznikach matematycznych, trójkąt o kątach 90, 30 i 60 stopni miał nazwę "piękny". Zaznaczam miał nazwę, bo obecnie tak się nie nazywa tego trójkąta. Potwierdzenia tej nazwy jest dla mnie ważne. Dziękuję jeśli Państwo odnajdziecie. Na pewno będą to podręczniki dla szkół średnich okresu przedwojennego, czyli przed 1939 rokiem.
2015-12-07 13:22:28 janeczka napisał(a):
Pytanie dotyczy poprzedniego - czyli czy trójkąt prostokątny nosi nazwę "piękny". Dawno, kilkanaście lat wstecz miałam podręcznik z lat przed 1939r. W nim przeczytałam tę nazwę, ale podręcznik nie zachował się. Nazwa była w internecie, a tera jako takiej nie mogę odszukać. jest to bardzo potrzebne do korzystania bezpośrednio z jego własności, bez dodatkowych obliczeń. Dlatego poszukuję potwierdzenia. Dziękuję za pomoc i oczekuję pilnie.
2015-12-08 12:36:54 janeczka napisał(a):
Ślicznie dziękuję, bo dzięki Wam Śzanowni Pastwo mam informację o trójkącie pięknym. Ukłony dla Was.