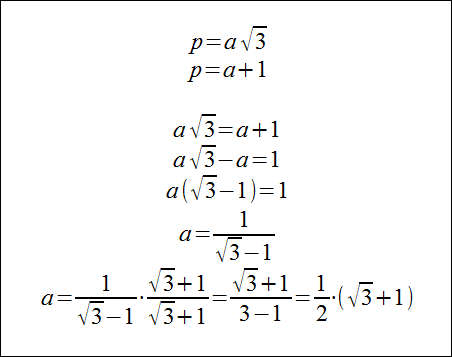Strona główna > Matematyka > Geometria przestrzenna > Przekątna sześcianu

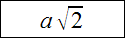
Wysokość sześcianu, jego przekątna i przekątna podstawy tworzą trójkąt prostokątny. Stosując twierdzenie Pitagorasa otrzymujemy:
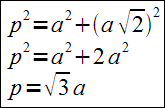
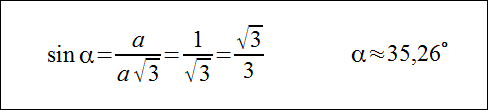
Oblicz długość przekątnej sześcianu o długości krawędzi a=2.
Rozwiązanie
Stosujemy podany wzór:
d=2*pierwiastek z 3
Zadanie 2
Przekątna sześcianu jest o 1 dłuższa od jego krawędzi. Oblicz długość krawędzi.
Rozwiązanie
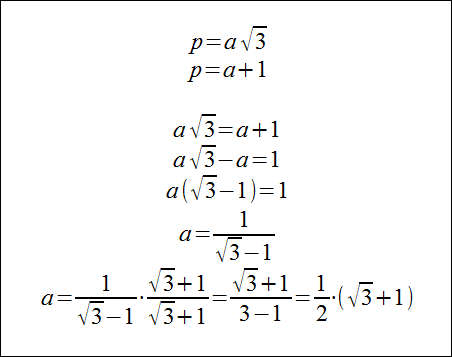
Przekątna sześcianu.
Dla sześcianu o krawędzi długości a jego przekątna p ma długość:
Przekątna sześcianu - uzasadnienie.
Niech będzie dany sześcian o krawędzi długości a. Oznaczmy przekątną sześcianu jako p. Podstawą sześcianu jest kwadrat. Przekątna kwadratu ma długość:Wysokość sześcianu, jego przekątna i przekątna podstawy tworzą trójkąt prostokątny. Stosując twierdzenie Pitagorasa otrzymujemy:
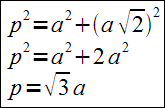
Kąt nachylenia przekątnej sześcianu do podstawy
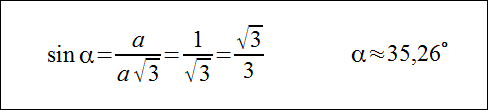
Przekątna sześcianu - zadania
Zadanie 1Oblicz długość przekątnej sześcianu o długości krawędzi a=2.
Rozwiązanie
Stosujemy podany wzór:
d=2*pierwiastek z 3
Zadanie 2
Przekątna sześcianu jest o 1 dłuższa od jego krawędzi. Oblicz długość krawędzi.
Rozwiązanie