Strona główna > Matematyka > Liczby zespolone > Liczby zespolone
W matematyce wprowadzano kolejne podzbiory liczb po to aby były w nich wykonywalne pewne działania. I tak na przykład ze względu na to, że w zbiorze liczb naturalnych nie były wykonywalne niektóre odejmowania wprowadzono liczby całkowite. Zbiór liczb zespolonych został wprowadzony ze względu na to, że w zbiorze liczb rzeczywistych nie można było wykonywać pierwiastkowania liczb ujemnych. Liczby zespolone mają postać: a+b*i gdzie i jest równe pierwiastkowi z -1 i nazywa się jednostką urojoną. Liczba a jest nazywana częścią rzeczywistą, liczba b częścią urojoną.


to kąt φ nazywamy argumentem liczby zespolonej z.
z=a+bi=|z|(cos φ + i*sin φ )
(a+bi) + (c+di) = (a+c)+ (b+d)*i
(a+bi) - (c+di) = (a-c)+ (b-d)*i
Rozwiązanie
z1+z22+3i+1-i=3+2i
z1-z22+3i-(1-i)=1+2i
z1 * z2=(a+b*i)(c+d*i)=ac+ad*i+bc*i-bd=(ac-bd)+i*(ad+bc)
Rozwiązanie
z1*z2=(1+2i)(1-3i)=1-3i+2i+6=7-i
Należy wykonać dzielenie (1+2i)/(3+i).
Rozwiązanie
W pierwszej kolejności mnożymy licznik i mianownik przez liczbę sprzężoną mianownika:
(1+2i)/(3+i) = (1+2i)(3-i)/[(3+i)(3-i)]
i wykonujemy odpowiednie mnożenia w liczniku i mianowniku:
(3-i+6i+2)/(9+1)=(5+5i)/(10)=0.5+0.5i
z = |z|(cos φ + i*sin φ )
n-ta potęga dana jest wzorem:
zn= |z|n(cos nφ + i*sin nφ )
Rozwiązanie
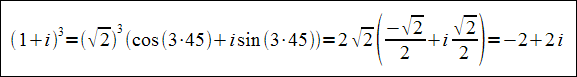
z = |z|(cos φ + i*sin φ )
Pierwiastek n-tego stopnia dany jest wzorem:
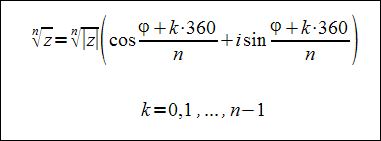
Rozwiązanie
Szukany pierwiastek ma dwie wartości:
1.09868 + 0.45509 i
-1.09868 + -0.45509 i
Pobierz program
2012-10-06 21:23:04 Magda napisał(a):
Witam! Dopiero zaczynam moją przygodę z liczbami zespolonymi i kompletnie nie wiem jak obliczyć: pierwiastek drugiego stopnia z (i-3). Pomocy! Dzięki za pomoc, MD.
Pojęcie liczby zespolonej
Zobacz także Liczby zespolone zadaniaW matematyce wprowadzano kolejne podzbiory liczb po to aby były w nich wykonywalne pewne działania. I tak na przykład ze względu na to, że w zbiorze liczb naturalnych nie były wykonywalne niektóre odejmowania wprowadzono liczby całkowite. Zbiór liczb zespolonych został wprowadzony ze względu na to, że w zbiorze liczb rzeczywistych nie można było wykonywać pierwiastkowania liczb ujemnych. Liczby zespolone mają postać: a+b*i gdzie i jest równe pierwiastkowi z -1 i nazywa się jednostką urojoną. Liczba a jest nazywana częścią rzeczywistą, liczba b częścią urojoną.
Moduł liczby zespolonej
Niech będzie dana liczba zespolona z postaci a+b*i. Modułem liczby zespolonej z nazywamy wyrażenie:
Argument liczby zespolonej
Jeśli liczbę zespoloną z=a+bi przedstawimy w postaci pokazanej na rysunku:
to kąt φ nazywamy argumentem liczby zespolonej z.
Postać trygonometryczna liczb zespolonych
Dowolną liczbę zespoloną z można przedstawić w postaci:z=a+bi=|z|(cos φ + i*sin φ )
Liczba sprzężona
Niech będzie dana liczba zespolona z postaci a+b*i. Liczbą sprzężoną nazywamy liczbę zespoloną postaci a-b*i.Dodawanie i odejmowanie liczb zespolonych
Dodawanie (odejmowanie) liczb zespolonych przeprowadzamy w ten sposób, że dodajemy (odejmujemy) części rzeczywiste i urojone odpowiednich liczb. Poniżej pokazano dodawanie i odejmowanie dwu liczb: a+bi oraz c+di:(a+bi) + (c+di) = (a+c)+ (b+d)*i
(a+bi) - (c+di) = (a-c)+ (b-d)*i
Przykład dodawania / odejmowania liczb zespolonych
Należy obliczyć sumę i różnicę (z1-z2) liczb z1=(2+3i) ,z2=(1-i).Rozwiązanie
z1+z22+3i+1-i=3+2i
z1-z22+3i-(1-i)=1+2i
Mnożenie liczb zespolonych
Niech dane będą dwie liczby zespolone z1=a+bi oraz z2=c+di. Iloczyn liczb z1,z2 przeprowadzamy następująco:z1 * z2=(a+b*i)(c+d*i)=ac+ad*i+bc*i-bd=(ac-bd)+i*(ad+bc)
Przykład mnożenia liczb zespolonych
Należy wykonać mnożenie liczb z1=1+2i oraz z2=1-3iRozwiązanie
z1*z2=(1+2i)(1-3i)=1-3i+2i+6=7-i
Dzielenie liczb zespolonych
Przykład dzielenia liczb zespolonychNależy wykonać dzielenie (1+2i)/(3+i).
Rozwiązanie
W pierwszej kolejności mnożymy licznik i mianownik przez liczbę sprzężoną mianownika:
(1+2i)/(3+i) = (1+2i)(3-i)/[(3+i)(3-i)]
i wykonujemy odpowiednie mnożenia w liczniku i mianowniku:
(3-i+6i+2)/(9+1)=(5+5i)/(10)=0.5+0.5i
Potęgowanie liczb zespolonych
Dla liczby zespolonej w postaci trygonometrycznej:z = |z|(cos φ + i*sin φ )
n-ta potęga dana jest wzorem:
zn= |z|n(cos nφ + i*sin nφ )
Przykład potęgowania liczby zespolonej
Należy obliczyć (1+i)3Rozwiązanie
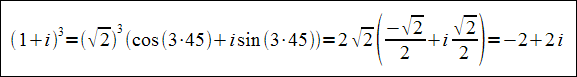
Pierwiastkowanie liczb zespolonych
Dla liczby zespolonej w postaci trygonometrycznej:z = |z|(cos φ + i*sin φ )
Pierwiastek n-tego stopnia dany jest wzorem:
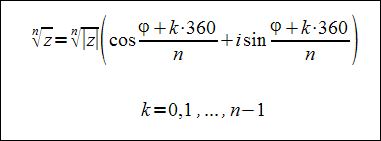
Pierwiastkowanie liczb zespolonych - przykład
Należy obliczyć pierwiastek drugiego stopnia z liczby 1+i.Rozwiązanie
Szukany pierwiastek ma dwie wartości:
1.09868 + 0.45509 i
-1.09868 + -0.45509 i
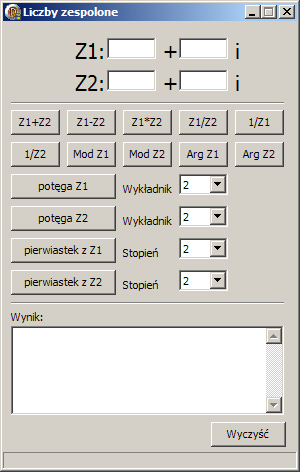
Kalkulator liczb zespolonych
Przedstawiamy prosty kalkulator pozwalający na dodawanie,odejmowanie,mnożenie, dzielenie, podnoszenie do potęgi, pierwiastkowanie, obliczanie modułu i argumentu liczb zespolonych.Pobierz program

Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (1)
2012-10-06 21:23:04 Magda napisał(a):
Witam! Dopiero zaczynam moją przygodę z liczbami zespolonymi i kompletnie nie wiem jak obliczyć: pierwiastek drugiego stopnia z (i-3). Pomocy! Dzięki za pomoc, MD.