Strona główna > Matematyka > Geometria przestrzenna > Graniastosłup prawidłowy sześciokątny

Jest to graniastosłup prosty, którego podstawą jest sześciokąt foremny.
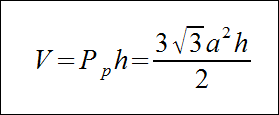
W powyższym wzorze a oznacza długość krawędzi podstawy graniastosłupa, h - wysokość graniastosłupa.
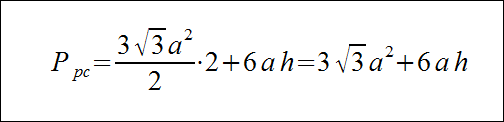


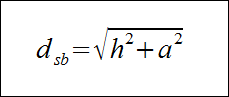
Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 4 i wysokości 8. Oblicz jego objętość.
Rozwiązanie
Zgodnie ze wzorem na objętość graniastosłupa prawidłowego 6-kątnego otrzymujemy:
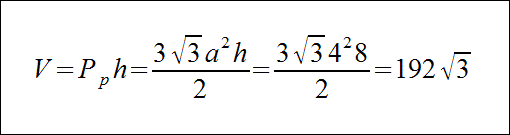
Zadanie 2
Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 5 i wysokości 12. Oblicz jego pole powierzchni całkowitej.
Rozwiązanie
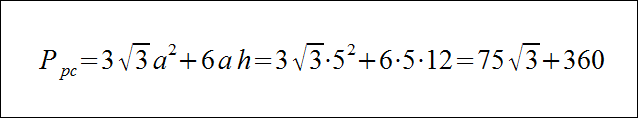
Zadanie 3
Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 6 i objętości 40. Oblicz jego wysokość.
Rozwiązanie
Aby rozwiązać zadanie przekształcamy wzór na objętość tak, aby wyznaczyć z niego wysokość h:

Po wstawieniu danych otrzymujemy:
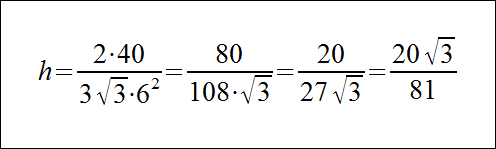
Zadanie 4
Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 5 i objętości 100. Oblicz jego dłuższą przekątną tego graniastosłupa.
Rozwiązanie 4
Najpierw liczymy wysokość graniastosłupa:
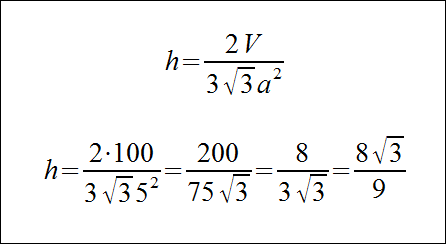
Następnie obliczamy długość przekątnej:
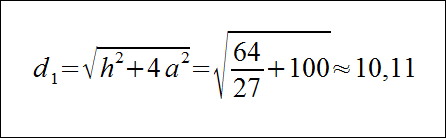
2012-09-05 17:05:50 katharina napisał(a):
to jest bardzo pomocne przydaje się
2013-03-13 16:40:41 koninka1 napisał(a):
Bardzo przydatne informacje.
2013-05-22 19:54:39 nie kumałam tego ;( napisał(a):
Dziękuję bardzo za wytłumaczenie może chociaż trochę bardziej to zrozumiem :)polecam ;)
2015-10-29 17:00:54 karina napisał(a):
Szklane akwarium ma kształt prawidłowego graniastosłupa sześciokątnego o wysokości 4dm oraz krawędzi podstawy 2dm. Z ilu metrów kwadratowych szkła jest wykonane akwarium?
Graniastosłup prawidłowy sześciokątny

Jest to graniastosłup prosty, którego podstawą jest sześciokąt foremny.
Graniastosłup prawidłowy sześciokątny - wzór na objętość
Objętość dowolnego graniastosłupa to iloczyn pola podstawy razy wysokość. Ze względu na to, że podstawą jest sześciokąt foremny to objętość będzie równa polu sześciokąta foremnego razy wysokość graniastosłupa: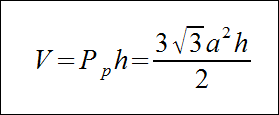
W powyższym wzorze a oznacza długość krawędzi podstawy graniastosłupa, h - wysokość graniastosłupa.
Graniastosłup prawidłowy sześciokątny - wzór na pole powierzchni całkowitej
Pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego jest równe: 2 * pole podstawy + 6 * pole ściany bocznej. Wyraża to następujący wzór: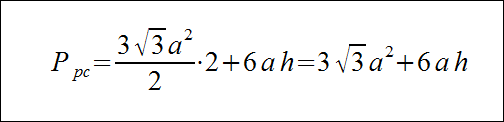
Pole podstawy graniastosłupa prawidłowego sześciokątnego
Podstawą graniastosłupa prawidłowego 6-kątnego jest sześciokąt foremny. Stąd pole podstawy jest równe:
Długości przekątnych graniastosłupa prawidłowego sześciokątnego

Długości przekątnych ścian bocznych graniastosłupa prawidłowego sześciokątnego
Długość przekątnej ściany bocznej liczymy stosując twierdzenie Pitagorasa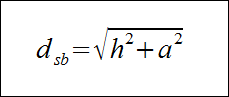
Graniastosłup prawidłowy sześciokątny - zadania
Zadanie 1Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 4 i wysokości 8. Oblicz jego objętość.
Rozwiązanie
Zgodnie ze wzorem na objętość graniastosłupa prawidłowego 6-kątnego otrzymujemy:
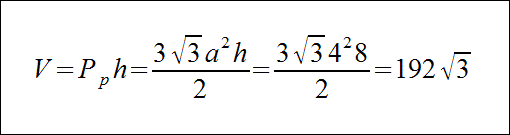
Zadanie 2
Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 5 i wysokości 12. Oblicz jego pole powierzchni całkowitej.
Rozwiązanie
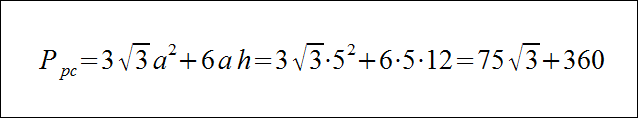
Zadanie 3
Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 6 i objętości 40. Oblicz jego wysokość.
Rozwiązanie
Aby rozwiązać zadanie przekształcamy wzór na objętość tak, aby wyznaczyć z niego wysokość h:

Po wstawieniu danych otrzymujemy:
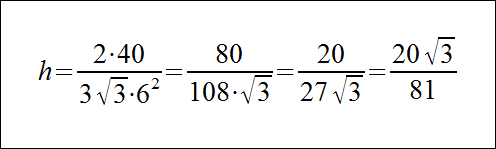
Zadanie 4
Dany jest graniastosłup prawidłowy sześciokątny o długości krawędzi podstawy równej 5 i objętości 100. Oblicz jego dłuższą przekątną tego graniastosłupa.
Rozwiązanie 4
Najpierw liczymy wysokość graniastosłupa:
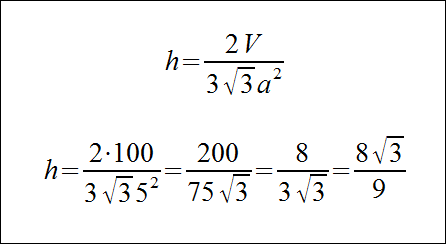
Następnie obliczamy długość przekątnej:
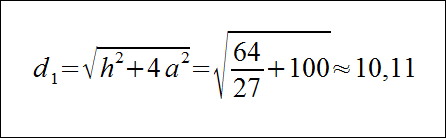
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (4)
2012-09-05 17:05:50 katharina napisał(a):
to jest bardzo pomocne przydaje się
2013-03-13 16:40:41 koninka1 napisał(a):
Bardzo przydatne informacje.
2013-05-22 19:54:39 nie kumałam tego ;( napisał(a):
Dziękuję bardzo za wytłumaczenie może chociaż trochę bardziej to zrozumiem :)polecam ;)
2015-10-29 17:00:54 karina napisał(a):
Szklane akwarium ma kształt prawidłowego graniastosłupa sześciokątnego o wysokości 4dm oraz krawędzi podstawy 2dm. Z ilu metrów kwadratowych szkła jest wykonane akwarium?