Strona główna > Matematyka > Geometria przestrzenna > Wzór na pole powierzchni całkowitej walca

Pole powierzchni całkowitej walca jest równe sumie pól podstaw i powierzchni bocznej walca. Pole podstawy Pp walca o promieniu r jest równe:
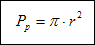
Pole powierzchni bocznej Ppb walca jest równe:

Zatem pole powierzchni całkowitej walca jest równe:

pi=3,1415926535897932384626433832795
Rozwiązanie :Jeśli obrócimy prostokąt wokół boku b to powstały walec będzie miał promień podstawy r = a = 2, wysokość h = b = 4. Stąd pole powierzchni całkowitej walca będzie równe: P = 2 * π * r (r+h)= 2 * π * 2 * (2+4) = 24 π
2015-10-29 17:07:12 karina napisał(a):
Kolumna ma kształt walca o wysokości 40dm. i średnicy podstawy ok0,6m, Ile puszek farby trzeba kupić na pomalowanie powierzchni bocznej dziesięciu takich kolumn, jeśli 1 puszka tej farby wystarcza na 6m kwadratowych powierzchni?
2015-10-29 20:13:25 Krzysztof napisał(a):
Hej. Pole powierzchni bocznej walca jest równe 2 * pi * r* h . W zadaniu h=40 dm=0,4m. Mamy więc: Ppb=2*pi*0.6*0.4=2*3.14*0.6*0.4 = 1.507. 10 kolumn będzie miało powierzchnię 15.07 m2. Ilość puszek: 15.07/6 = 2.51 - zaokrąglamy w górę do 3. Odp.: Na pomalowanie kolumn potrzeba 3 puszek farby.
Wzór na pole powierzchni całkowitej walca

Pole powierzchni całkowitej walca jest równe sumie pól podstaw i powierzchni bocznej walca. Pole podstawy Pp walca o promieniu r jest równe:
Pole powierzchni bocznej Ppb walca jest równe:
Zatem pole powierzchni całkowitej walca jest równe:
pi=3,1415926535897932384626433832795
Zadania
Zadanie 1:Dany jest prostokąt o wymiarach a=2, b=4. Prostokąt ten obrócono wokół osi, która zawiera się w dłuższym boku. Oblicz pole powierzchni całkowitej powstałego walca.Rozwiązanie :Jeśli obrócimy prostokąt wokół boku b to powstały walec będzie miał promień podstawy r = a = 2, wysokość h = b = 4. Stąd pole powierzchni całkowitej walca będzie równe: P = 2 * π * r (r+h)= 2 * π * 2 * (2+4) = 24 π
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (2)
2015-10-29 17:07:12 karina napisał(a):
Kolumna ma kształt walca o wysokości 40dm. i średnicy podstawy ok0,6m, Ile puszek farby trzeba kupić na pomalowanie powierzchni bocznej dziesięciu takich kolumn, jeśli 1 puszka tej farby wystarcza na 6m kwadratowych powierzchni?
2015-10-29 20:13:25 Krzysztof napisał(a):
Hej. Pole powierzchni bocznej walca jest równe 2 * pi * r* h . W zadaniu h=40 dm=0,4m. Mamy więc: Ppb=2*pi*0.6*0.4=2*3.14*0.6*0.4 = 1.507. 10 kolumn będzie miało powierzchnię 15.07 m2. Ilość puszek: 15.07/6 = 2.51 - zaokrąglamy w górę do 3. Odp.: Na pomalowanie kolumn potrzeba 3 puszek farby.