Strona główna > Matematyka > Geometria płaszczyzny > Trójkąt prostokątny równoramienny, trójkąt 45 45 90






1. Rysujemy prostą i zaznaczamy na niej punkt A, w którym będzie się znajdować wierzchołek kąta prostego.

2. Za pomocą cyrkla zaznaczamy po obu stronach punktu A dwa punkty B i C równoodległe od A.
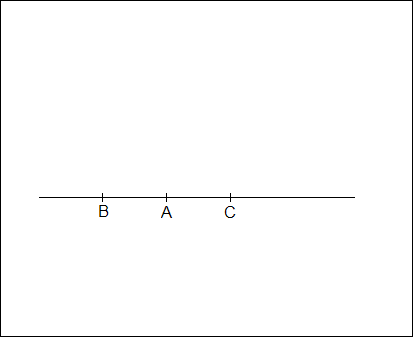
3. Konstruujemy symetralną odcinka BC : rozwartością cyrkla większą od połowy długości odc. BC rysujemy dwa okręgi. Środek pierwszego to punkt B a środek drugiego to punkt C.

Łączymy miejsca przecięcia się okręgów.

Korzystając z cyrkla odkładamy na powstałym kącie przyprostokątne danego trójkąta i łączymy końce przyprostokątnych otrzymując trójkąt prostokątny.
2013-03-03 01:37:14 megi333 napisał(a):
Jaką ma długość przyprostokątna równoramiennego trójkąta prostokątnego o obwodzie 2?
2013-03-03 02:57:28 BazyWiedzy.COM napisał(a):
Witaj.
Jeśli przyprostokątne w równoramiennym trójkącie prostokątnym oznaczymy jako a to przeciwprostokątna będzie miała długość a √ 2. Stąd możemy zapisać równanie:
a+a+a*√ 2=2
a*(2+√ 2)=2
a=2/(2+√ 2)
Usuwamy niewymierność z mianownika:
a=2/(2+√ 2) = 2/(2+√ 2) * (2 - √ 2)/(2-√ 2) = 2 - √ 2
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-05-03 16:55:42 Tomek 222 napisał(a):
W trójkącie prostokątnym równoramiennym najkrótsza wysokość ,a długość 1 dm.Oblicz długości boków tego trójkąta.
2013-05-04 15:20:38 BazyWiedzy.COM napisał(a):
Trójkąt prostokątny równoramienny ma trzy wysokości: dwie mają tą samą długość i zawierają się w przyprostokątnych. Trzecia wysokość (najkrótsza) jest opuszczona na przeciwprostokątną. Jeśli jako a oznaczymy przyprostokątną to ta trzecia wysokość będzie miała długość √2 a/2. Stąd mamy:
√2/2 a = 1
a=2/√2 = √2
Przeciwprostokątna ma długość: b=√2 a = √2 * √2 = 2
Pozdrawiam - Marcin
2024-11-17 07:23:43 Aneta napisał(a):
Witaj. Zadanie bez rysunku. Oblicz pole trójkąta równoramiennego, którego kąty ostre mają po 45st., a podstawa jest równa 14cm. Czy w tej sytuacji bierzemy podstawę między ramionami i wówczas P=49cm2 czy też jedną z przyprostokątnych i wtedy P=98cm2?
Trójkąt prostokątny równoramienny, trójkąt 45 45 90
Trójkąt prostokątny równoramienny to taki trójkąt, w którym kąty mają miary 90,45,45 stopni. W trójkącie takim ramiona kąta 90 stopni mają równą długość. Jeśli przez a oznaczymy równe ramiona przez, c - trzeci bok trójkąta to stosując twierdzenie Pitagorasa możemy wyznaczyć c:

Wysokości w trójkącie prostokątnym równoramiennym (trójkącie 45 45 90)
Obydwie przyprostokątne a są jednocześnie wysokościami trójkąta. Trzecia wysokość dzieli przeciwprostokątną na dwa równe odcinki. Wysokość ta ma długość:
Pole trójkąta prostokątnego równoramiennego (trójkąta 45 45 90)

Obwód trójkąta prostokątnego równoramiennego (trójkąta 45 45 90)

Promień okręgu opisanego na trójkącie prostokątnym równoramiennym (trójkącie 45 45 90)
Jeśli na trójkącie prostokątnym opiszemy okrąg to jego średnica będzie równa przeciwprostokątnej. Dlatego promień okręgu opisanego na trójkącie prostokątnym równoramiennym o przyprostokątnej a jest równy:
Konstrukcja trójkąta prostokątnego równoramiennego (trójkąta 45 45 90)
Aby skonstruować trójkąt prostokątny wykonujemy następujące kroki:1. Rysujemy prostą i zaznaczamy na niej punkt A, w którym będzie się znajdować wierzchołek kąta prostego.

2. Za pomocą cyrkla zaznaczamy po obu stronach punktu A dwa punkty B i C równoodległe od A.
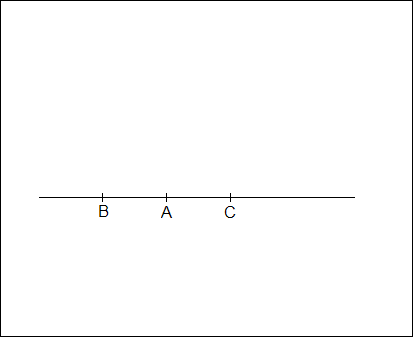
3. Konstruujemy symetralną odcinka BC : rozwartością cyrkla większą od połowy długości odc. BC rysujemy dwa okręgi. Środek pierwszego to punkt B a środek drugiego to punkt C.

Łączymy miejsca przecięcia się okręgów.

Korzystając z cyrkla odkładamy na powstałym kącie przyprostokątne danego trójkąta i łączymy końce przyprostokątnych otrzymując trójkąt prostokątny.
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (5)
2013-03-03 01:37:14 megi333 napisał(a):
Jaką ma długość przyprostokątna równoramiennego trójkąta prostokątnego o obwodzie 2?
2013-03-03 02:57:28 BazyWiedzy.COM napisał(a):
Witaj.
Jeśli przyprostokątne w równoramiennym trójkącie prostokątnym oznaczymy jako a to przeciwprostokątna będzie miała długość a √ 2. Stąd możemy zapisać równanie:
a+a+a*√ 2=2
a*(2+√ 2)=2
a=2/(2+√ 2)
Usuwamy niewymierność z mianownika:
a=2/(2+√ 2) = 2/(2+√ 2) * (2 - √ 2)/(2-√ 2) = 2 - √ 2
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-05-03 16:55:42 Tomek 222 napisał(a):
W trójkącie prostokątnym równoramiennym najkrótsza wysokość ,a długość 1 dm.Oblicz długości boków tego trójkąta.
2013-05-04 15:20:38 BazyWiedzy.COM napisał(a):
Trójkąt prostokątny równoramienny ma trzy wysokości: dwie mają tą samą długość i zawierają się w przyprostokątnych. Trzecia wysokość (najkrótsza) jest opuszczona na przeciwprostokątną. Jeśli jako a oznaczymy przyprostokątną to ta trzecia wysokość będzie miała długość √2 a/2. Stąd mamy:
√2/2 a = 1
a=2/√2 = √2
Przeciwprostokątna ma długość: b=√2 a = √2 * √2 = 2
Pozdrawiam - Marcin
2024-11-17 07:23:43 Aneta napisał(a):
Witaj. Zadanie bez rysunku. Oblicz pole trójkąta równoramiennego, którego kąty ostre mają po 45st., a podstawa jest równa 14cm. Czy w tej sytuacji bierzemy podstawę między ramionami i wówczas P=49cm2 czy też jedną z przyprostokątnych i wtedy P=98cm2?