Strona główna > Matematyka > Geometria w układzie xy > Symetralna odcinka

Po pierwsze wyznaczamy równanie prostej AB z wzoru:
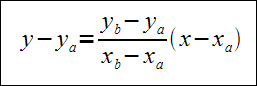
y-2=(4-2)/(3-1) * (x-1)
y-2=2/2 * (x-1)
y-2=x-1
y=x-1+2
y=x+1
Następnie wyznaczamy równanie prostej prostopadłej. Wiadomo, że jeśli dwie proste są prostopadłe to iloczyn ich współczynników kierunkowych jest równy -1. Dlatego nasza prosta prostopadła będzie miała wzór:
y=-x+b
Współczynnik b nie jest znany ponieważ istnieje nieskończenie wiele prostych prostopadłych do danej prostej. Musimy wyznaczyć wartość tego współczynnika wiedząc, że prosta prostopadła do AB przechodzi przez S.
Wyznaczmy najpierw współrzędne środka odcinka AB:
xs=(xa+xb)/2=4/2=2
ys=(ya+yb)/2=6/2=3
S(2,3)
Jeśli S ma należeć do symetralnej to współrzędne punktu S muszą spełniać równanie symetralnej:
y=-x+b
3=-2+b
5=b
b=5
Szukane równanie symetralnej jest więc następujące:
y=-x+5

Aby narysować symetralną odcinka AB należy wykonać następujące kroki:
1. Rysujemy dwa okręgi o środkach w końcach odcinka AB i o dowolnym promieniu większym od połowy długości odcinka:

2. Następnie prowadzimy prostą przechodzącą przez punkty przecięcia okręgów:

Prosta ta będzie symetralną odcinka AB.
2012-06-26 17:20:37 Marlena napisał(a):
Przydatne ; dd
2013-03-17 08:47:45 Aga080692 napisał(a):
proszę o pomoc
1.wyznacz równanie prostej symetralnej odcinka AB o końcach a(-2,3) b (6,-1)
2. napisz równanie prostej prostopadłej do 5x-3y+1=0 przechodzącej przez P(3,-2)
2013-03-17 19:28:31 BazyWiedzy.COM napisał(a):
Witaj.
Zadanie 1.
Najpierw wyznaczamy równanie prostej AB:
A(-2,3) , B (6,-1)
y-3=[(-1-3)/(6--2)] * (x--2)
y-3=-4/8 * (x+2)
y-3=-0.5x -1
y=-0.5*x +2
Teraz wyznaczamy współrzędne środka odcinka AB (przez ten punkt będzie przechodzić symetralna):
xs = (xa+xb)/2 = (-2+6)/2=2
ys = (ya+yb)/2 = (3-1)/2=1
Symetralna będzie prostą prostopadłą do y=-0.5*x +2 przechodzącą przez punkt S(2,1). Z warunku na prostopadłość wynika, że symetralna będzie miała równanie y=2*x+b. Jeśli S należy do symetralnej to współrzędne tego punktu muszą spełniać równanie symetralnej:
1=2*2+b
1-4=b
b=-3
Stąd równanie symetralnej:
y=2*x-3
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-17 20:49:41 BazyWiedzy.COM napisał(a):
Zadanie 2.
Przekształcamy równanie prostej do postaci kierunkowej:
5x-3y+1=0
5x+1=3y
y=(5/3) * x + 1/3
Prosta prostopadła do danej będzie miała równanie:
y=-(3/5) * x + b
Jeśli wiadomo, że do prostej należy punkt P(3,-2) to:
-2=-(3/5) * 3 + b
-2+9/5 = b
b=-1/5
Stąd równanie szukanej prostej:
y=-(3/5) * x -1/5
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-04-16 21:01:30 zielona napisał(a):
Na symetralnej odcinka AB, gdzie A=(1,2), B=(-3,0), znajdź punkt wspólny z prostą 2x-y+3=0. Proszę o pomoc..
2013-04-17 01:29:10 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie:

2013-04-29 17:54:23 Monisza0609 napisał(a):
Dziękuję bardzo za symetralną odcinka :) Pozdrawiam .
Symetralna odcinka.
Symetralna odcinka AB to prosta prostopadła do prostej zawierającej odcinek AB i przechodząca przez jego środek. Na rysunku pokazano symetralną odcinka AB. Środek odcinka oznaczono tutaj jako S. Symetralna odcinka AB to prosta k.
Przykład wyznaczania równania symetralnej odcinka.
Niech dany będzie odcinek AB o końcach w punktach A(1,2) i B(3,4). Należy wyznaczyć równanie symetralnej odcinka AB.Po pierwsze wyznaczamy równanie prostej AB z wzoru:
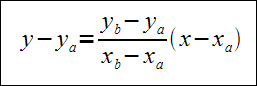
y-2=(4-2)/(3-1) * (x-1)
y-2=2/2 * (x-1)
y-2=x-1
y=x-1+2
y=x+1
Następnie wyznaczamy równanie prostej prostopadłej. Wiadomo, że jeśli dwie proste są prostopadłe to iloczyn ich współczynników kierunkowych jest równy -1. Dlatego nasza prosta prostopadła będzie miała wzór:
y=-x+b
Współczynnik b nie jest znany ponieważ istnieje nieskończenie wiele prostych prostopadłych do danej prostej. Musimy wyznaczyć wartość tego współczynnika wiedząc, że prosta prostopadła do AB przechodzi przez S.
Wyznaczmy najpierw współrzędne środka odcinka AB:
xs=(xa+xb)/2=4/2=2
ys=(ya+yb)/2=6/2=3
S(2,3)
Jeśli S ma należeć do symetralnej to współrzędne punktu S muszą spełniać równanie symetralnej:
y=-x+b
3=-2+b
5=b
b=5
Szukane równanie symetralnej jest więc następujące:
y=-x+5
Konstrukcja symetralnej odcinka.
Niech dany będzie odcinek pokazany na rysunku.
Aby narysować symetralną odcinka AB należy wykonać następujące kroki:
1. Rysujemy dwa okręgi o środkach w końcach odcinka AB i o dowolnym promieniu większym od połowy długości odcinka:

2. Następnie prowadzimy prostą przechodzącą przez punkty przecięcia okręgów:

Prosta ta będzie symetralną odcinka AB.
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (7)
2012-06-26 17:20:37 Marlena napisał(a):
Przydatne ; dd
2013-03-17 08:47:45 Aga080692 napisał(a):
proszę o pomoc
1.wyznacz równanie prostej symetralnej odcinka AB o końcach a(-2,3) b (6,-1)
2. napisz równanie prostej prostopadłej do 5x-3y+1=0 przechodzącej przez P(3,-2)
2013-03-17 19:28:31 BazyWiedzy.COM napisał(a):
Witaj.
Zadanie 1.
Najpierw wyznaczamy równanie prostej AB:
A(-2,3) , B (6,-1)
y-3=[(-1-3)/(6--2)] * (x--2)
y-3=-4/8 * (x+2)
y-3=-0.5x -1
y=-0.5*x +2
Teraz wyznaczamy współrzędne środka odcinka AB (przez ten punkt będzie przechodzić symetralna):
xs = (xa+xb)/2 = (-2+6)/2=2
ys = (ya+yb)/2 = (3-1)/2=1
Symetralna będzie prostą prostopadłą do y=-0.5*x +2 przechodzącą przez punkt S(2,1). Z warunku na prostopadłość wynika, że symetralna będzie miała równanie y=2*x+b. Jeśli S należy do symetralnej to współrzędne tego punktu muszą spełniać równanie symetralnej:
1=2*2+b
1-4=b
b=-3
Stąd równanie symetralnej:
y=2*x-3
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-17 20:49:41 BazyWiedzy.COM napisał(a):
Zadanie 2.
Przekształcamy równanie prostej do postaci kierunkowej:
5x-3y+1=0
5x+1=3y
y=(5/3) * x + 1/3
Prosta prostopadła do danej będzie miała równanie:
y=-(3/5) * x + b
Jeśli wiadomo, że do prostej należy punkt P(3,-2) to:
-2=-(3/5) * 3 + b
-2+9/5 = b
b=-1/5
Stąd równanie szukanej prostej:
y=-(3/5) * x -1/5
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-04-16 21:01:30 zielona napisał(a):
Na symetralnej odcinka AB, gdzie A=(1,2), B=(-3,0), znajdź punkt wspólny z prostą 2x-y+3=0. Proszę o pomoc..
2013-04-17 01:29:10 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie:

2013-04-29 17:54:23 Monisza0609 napisał(a):
Dziękuję bardzo za symetralną odcinka :) Pozdrawiam .