Strona główna > Matematyka > Równania i nierówności > Równania trygonometryczne
sin(x) = a
cos(x) = a
tg(x) = a
ctg(x) = a
Liczba a należy do R.
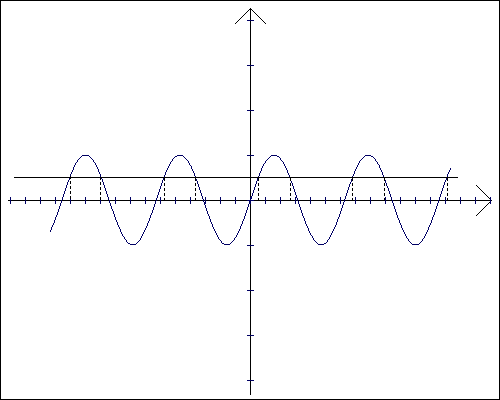
Ze względu na to, że okres funkcji sin(x) jest równy 2π to aby rozwiązać równanie sin(x)=a dla x należącego do R, najpierw należy znaleźć rozwiązania w przedziale < 0 , 2π >. Następnie do znalezionych rozwiązań dodajemy 2kπ gdzie k jest liczbą całkowitą.
Zadanie 1
Należy rozwiązać równanie sin(x)=0.5.
Rozwiązanie
Znajdujemy rozwiązania równania dla x należącego do < 0 , 2π >:
x= π/3 lub x = 5π/6
Po dodaniu składnika 2kπ ostateczne rozwiązanie równania ma postać:
x= π/3+2kπ lub x = 5π/6+2kπ
W przypadku równania elementarnego cos(x)=a postępujemy analogicznie.
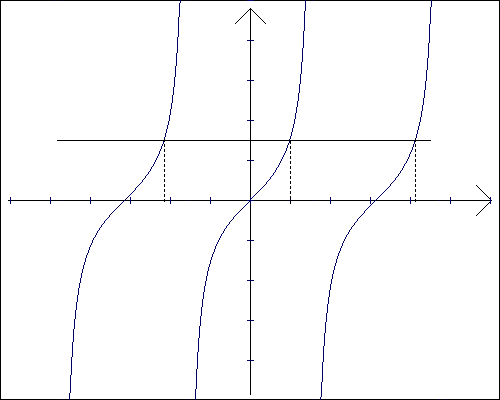
Ze względu na to, że okres funkcji tg(x) jest równy π to aby rozwiązać równanie tg(x)=a dla x należącego do R, najpierw należy znaleźć rozwiązania w przedziale < 0 , π >. Następnie do znalezionych rozwiązań dodajemy kπ gdzie k jest liczbą całkowitą.
Zadanie 2
Należy rozwiązać równanie tg(x)=1.
Rozwiązanie
Znajdujemy rozwiązania równania dla x należącego do < 0 , π >:
x=π/4
Dodajemy składnik kπ otrzymując ostateczne rozwiązanie równania:
x=π/4 + kπ
sin[g(x)] = sin[h(x)]
cos[g(x)] = cos[h(x)]
tg[g(x)] = tg[h(x)]
ctg[g(x)] = ctg[h(x)]
Zadanie 3
Należy rozwiązać równanie 2sin2(x)-sin(x)=0.
Rozwiązanie
Rozkładamy lewą stronę równania na czynniki:
2sin2(x)-sin(x)=0
sin(x)[2sin(x)-1]=0.
Aby to równanie było prawdziwe musi być spełniony warunek:
sin(x)=0 lub 2sin(x)-1=0
Aby pierwsze równanie było spełnione x=k Π.
Aby drugie równanie było spełnione:
2sin(x)-1=0
2sin(x)=1
sin(x)=0.5
Równanie to jest identyczne jak to z zadania 1. Jego rozwiązanie jest równe:
x= π/3+2kπ lub x = 5π/6+2kπ
Rozwiązanie równania 2sin2(x)-sin(x)=0 będzie sumą rozwiązań:
x= π/3+2kπ lub x = 5π/6+2kπ lub x=k Π przy czym k należy do zb. liczb całkowitych.
Elementarne równania trygonometryczne
Elementarne równania trygonometryczne mają postać:sin(x) = a
cos(x) = a
tg(x) = a
ctg(x) = a
Liczba a należy do R.
Równania sin(x)=a oraz cos(x)=a
Równanie to posiada rozwiązania tylko wtedy, gdy a należy do przedziału < -1 , 1 > Jeśli spełniony jest ten warunek i x należy do R, równanie sin(x)=a posiada nieskończenie wiele rozwiązań. Poniższy rysunek pokazuje interpretację geometryczną omawianego równania:
Ze względu na to, że okres funkcji sin(x) jest równy 2π to aby rozwiązać równanie sin(x)=a dla x należącego do R, najpierw należy znaleźć rozwiązania w przedziale < 0 , 2π >. Następnie do znalezionych rozwiązań dodajemy 2kπ gdzie k jest liczbą całkowitą.
Zadanie 1
Należy rozwiązać równanie sin(x)=0.5.
Rozwiązanie
Znajdujemy rozwiązania równania dla x należącego do < 0 , 2π >:
x= π/3 lub x = 5π/6
Po dodaniu składnika 2kπ ostateczne rozwiązanie równania ma postać:
x= π/3+2kπ lub x = 5π/6+2kπ
W przypadku równania elementarnego cos(x)=a postępujemy analogicznie.
Równania tg(x)=a oraz ctg(x)=a
Jeśli x należy do R to równania tg(x)=a oraz ctg(x)=a mają zawsze rozwiązania niezależnie od wartości a.
Ze względu na to, że okres funkcji tg(x) jest równy π to aby rozwiązać równanie tg(x)=a dla x należącego do R, najpierw należy znaleźć rozwiązania w przedziale < 0 , π >. Następnie do znalezionych rozwiązań dodajemy kπ gdzie k jest liczbą całkowitą.
Zadanie 2
Należy rozwiązać równanie tg(x)=1.
Rozwiązanie
Znajdujemy rozwiązania równania dla x należącego do < 0 , π >:
x=π/4
Dodajemy składnik kπ otrzymując ostateczne rozwiązanie równania:
x=π/4 + kπ
Nieelementarne równania trygonometryczne
Nieelementarne równania trygonometryczne to równania postaci:sin[g(x)] = sin[h(x)]
cos[g(x)] = cos[h(x)]
tg[g(x)] = tg[h(x)]
ctg[g(x)] = ctg[h(x)]
Zadanie 3
Należy rozwiązać równanie 2sin2(x)-sin(x)=0.
Rozwiązanie
Rozkładamy lewą stronę równania na czynniki:
2sin2(x)-sin(x)=0
sin(x)[2sin(x)-1]=0.
Aby to równanie było prawdziwe musi być spełniony warunek:
sin(x)=0 lub 2sin(x)-1=0
Aby pierwsze równanie było spełnione x=k Π.
Aby drugie równanie było spełnione:
2sin(x)-1=0
2sin(x)=1
sin(x)=0.5
Równanie to jest identyczne jak to z zadania 1. Jego rozwiązanie jest równe:
x= π/3+2kπ lub x = 5π/6+2kπ
Rozwiązanie równania 2sin2(x)-sin(x)=0 będzie sumą rozwiązań:
x= π/3+2kπ lub x = 5π/6+2kπ lub x=k Π przy czym k należy do zb. liczb całkowitych.