Strona główna > Matematyka > Wyrażenia algebraiczne > Przekształcanie wzorów
Przykład nr 1.
W przykładzie tym wyznaczymy masę substancji ms z wzoru na stężenie procentowe:
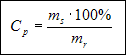
Rozwiązanie.
Dzielimy obydwie strony równania przez 100%:
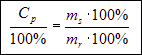
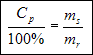
Mnożymy obydwie strony równania przez mr:
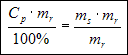
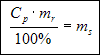
Przykład nr 2.
W przykładzie tym wyznaczymy masę substancji mr z wzoru na stężenie procentowe.
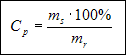
Rozwiązanie.
Mnożymy obydwie strony równania przez mr:
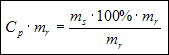
i skracamy prawą stronę przez mr:
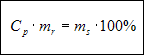
Dzielimy obydwie strony przez Cp
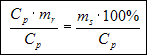
i skracamy lewą stronę przez Cp:
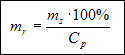
Przykład nr 3
Należy wyznaczyć z wzoru na pole trapezu długość podstawy a.
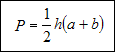
Przykład 4
Należy z twierdzenia Pitagorasa wyznaczyć długość boku c.
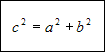
Rozwiązanie
Ponieważ obydwie strony są większe od 0 dlatego pierwiastkujemy obydwie strony równania:
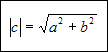
Ponieważ c > 0 dlatego można pominąć wartość bezwzględną:
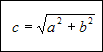
Przykład - przekształcanie wzoru z fizyki
Należy z wzoru na energię kinetyczną wyznaczyć prędkość.
Mnożymy obydwie strony wzoru przez 2.
Dzielimy obydwie strony wzoru przez masę m.
Pierwiastkujemy obydwie strony wzoru.
Operacje te pokazano poniżej:
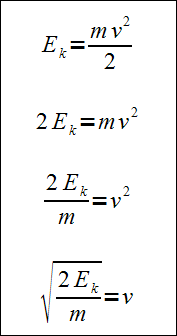
2012-06-18 19:47:45 Śliczna95 napisał(a):
Jak dla mnie to jest trudne: tłumaczyły mi to koleżanki i dalej nie za bardzo wiem o co w tym chodzi, jak mam przed sobą kartkę z przykładem to wiem skąd się co bierze ale jak mam sama robić to już nie za bardzo ;/.
2013-02-21 17:44:17 kateee napisał(a):
Bardzo proszę o pomoc w przekształceniu wzoru z fizyki, wyznaczyć t1=? q=mc(t2-t1) Z góry dziękuję.
2013-02-21 17:52:07 BazyWiedzy.COM napisał(a):
Witaj kateee :-)
Oto przekształcenie:
q=mc(t2-t1)
Dzielimy obustronnie przez mc:
q=mc(t2-t1) |:mc
"Przenosimy" t2 na lewą stronę:
q/(mc)-t2=-t1
Mnożymy obustronnie przez -1 aby po prawej stronie otrzymać t1:
q/(mc)-t2=-t1 | * (-1)
t2-q/(mc)=t1
Czyli możemy zapisać:
t1 = t2-q/(mc)
Pozdrawiam Cię
Marcin - BazyWiedzy.COM
Przekształcanie wzorów
Wzory w rozumieniu matematycznym są tym samym czym równania. Do przekształcania wzorów można więc wykorzystać te same twierdzenia co przy przekształcaniu równań matematycznych.Zasada nr 1 przekształcania wzorów
Dowolne równanie (obydwie jego strony) można pomnożyć lub podzielić przez tą samą liczbę (wyrażenie) różną (różne) od 0.Przykład nr 1.
W przykładzie tym wyznaczymy masę substancji ms z wzoru na stężenie procentowe:
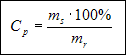
Rozwiązanie.
Dzielimy obydwie strony równania przez 100%:
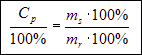
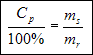
Mnożymy obydwie strony równania przez mr:
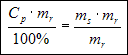
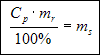
Przykład nr 2.
W przykładzie tym wyznaczymy masę substancji mr z wzoru na stężenie procentowe.
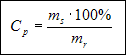
Rozwiązanie.
Mnożymy obydwie strony równania przez mr:
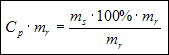
i skracamy prawą stronę przez mr:
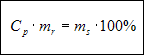
Dzielimy obydwie strony przez Cp
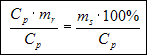
i skracamy lewą stronę przez Cp:
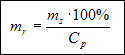
Zasada nr 2 przekształcania wzorów
Do obydwu stron dowolnego równania można dodać tą samą liczbę (wyrażenie) różną (różne) od 0. Od obydwu stron dowolnego równania można odjąć tą samą liczbę (wyrażenie) różną (różne) od 0.Przykład nr 3
Należy wyznaczyć z wzoru na pole trapezu długość podstawy a.
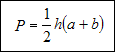
Zasada nr 3 przekształcania wzorów
Dowolne równanie można podnieść do potęgi 2 lub spierwiastkować pod warunkiem, że obydwie strony równania są > 0.Przykład 4
Należy z twierdzenia Pitagorasa wyznaczyć długość boku c.
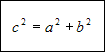
Rozwiązanie
Ponieważ obydwie strony są większe od 0 dlatego pierwiastkujemy obydwie strony równania:
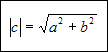
Ponieważ c > 0 dlatego można pominąć wartość bezwzględną:
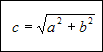
Przykład - przekształcanie wzoru z fizyki
Należy z wzoru na energię kinetyczną wyznaczyć prędkość.
Mnożymy obydwie strony wzoru przez 2.
Dzielimy obydwie strony wzoru przez masę m.
Pierwiastkujemy obydwie strony wzoru.
Operacje te pokazano poniżej:
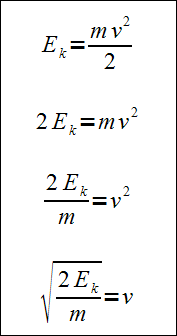
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (3)
2012-06-18 19:47:45 Śliczna95 napisał(a):
Jak dla mnie to jest trudne: tłumaczyły mi to koleżanki i dalej nie za bardzo wiem o co w tym chodzi, jak mam przed sobą kartkę z przykładem to wiem skąd się co bierze ale jak mam sama robić to już nie za bardzo ;/.
2013-02-21 17:44:17 kateee napisał(a):
Bardzo proszę o pomoc w przekształceniu wzoru z fizyki, wyznaczyć t1=? q=mc(t2-t1) Z góry dziękuję.
2013-02-21 17:52:07 BazyWiedzy.COM napisał(a):
Witaj kateee :-)
Oto przekształcenie:
q=mc(t2-t1)
Dzielimy obustronnie przez mc:
q=mc(t2-t1) |:mc
"Przenosimy" t2 na lewą stronę:
q/(mc)-t2=-t1
Mnożymy obustronnie przez -1 aby po prawej stronie otrzymać t1:
q/(mc)-t2=-t1 | * (-1)
t2-q/(mc)=t1
Czyli możemy zapisać:
t1 = t2-q/(mc)
Pozdrawiam Cię
Marcin - BazyWiedzy.COM