Strona główna > Matematyka > Geometria przestrzenna > Przekrój osiowy stożka

Dla stożka o promieniu podstawy r i wysokości h oraz tworzącej l przekrój osiowy jest trójkątem o bokach 2r,l,l . Pole przekroju osiowego jest równe iloczynowi promienia razy wysokość stożka co wyraża wzór:

Dany jest stożek o r=4 i h=3. Oblicz pole przekroju osiowego.
Rozwiązanie
P=r * h=4*3=12
Zadanie 2
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 6. Oblicz objętość stożka.
Rozwiązanie
Promień podstawy stożka, o którym mowa w zadaniu wynosi 3. Wyznaczmy wysokość stożka:

Znając teraz wysokość liczymy objętość stożka:
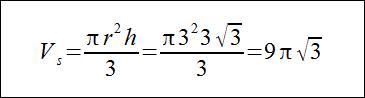
Zadanie 3
Przekrój osiowy stożka jest trójkątem prostokątnym o polu 2. Oblicz pole powierzchni bocznej stożka.
Rozwiązanie
Przekrój osiowy stożka obrotowego jest trójkątem równoramiennym. Jeśli jeden z jego kątów ma miarę 90 stopni to może to być tylko kąt rozwarcia. W zadaniu mamy zatem do czynienia z trójkątem o kątach 45,45,90. Pole takiego trójkąta będzie równe (l to długość tworzącej stożka) :

Obliczmy promień stożka. Przekrój osiowy jest trójkątem 90,45,45 co oznacza, że promień stożka będzie równy połowie przeciwprostokątnej tego trójkąta:
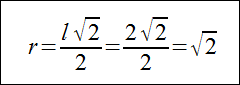
Teraz już możemy obliczyć pole powierzchni bocznej stożka:

Zadanie 4
Kąt rozwarcia stożka wynosi 120°. Oblicz pole przekroju osiowego tego stożka jeśli jego objętość jest równa (100 pi * √3 )/3.
Rozwiązanie
Jeśli kąt rozwarcia stożka jest równy 120° to tworząca, wysokość i promień podstawy tworzą trójkąt 30,60,90. Stąd otrzymujemy związek między h i r:
h/r = tg 30 °
Dodatkowo znając objętość możemy napisać równanie:
(100 pi * √3 )/3 = pi * r2 * h/3
Stąd otrzymujemy:

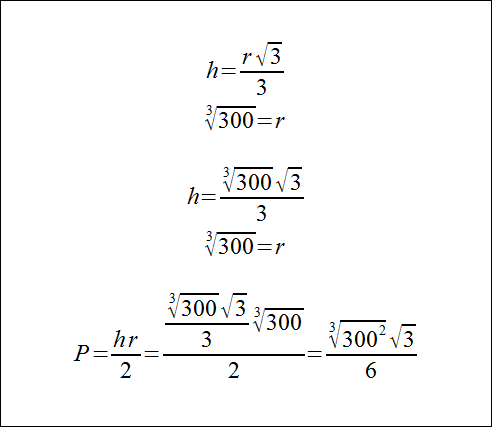
2013-03-24 18:48:24 Ania napisał(a):
Witam mam problem z zadaniem o treści:
W kulę wpisano stożek którego przekrojem osiowym jest trójkąt równoboczny o boku długości a=6cm. Oblicz objętość kuli i stożka.
Proszę o szybkie rozwiązanie zadanie potrzebne na wtorek :)
2013-03-24 20:00:13 ania napisał(a):
mam również problem z paroma innymi zadaniami i proszę o pomoc
2) w ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a=5cm. krawędź boczna ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 60 stopni. oblicz objętość i pole powierzchni całkowitej ostrosłupa
3) przekątna przekroju osiowego walca jest nachylona do wysokości pod kątem 30 stopni oblicz pole powierzchni walca i objętość jeżeli jego wysokość ma 8cm
2013-03-25 19:22:05 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie zadania:
Pozdrawiam
Marcin - BazyWiedzy.COM

Przekrój osiowy stożka
Przekrój osiowy stożka obrotowego zawiera w sobie średnicę podstawy i wysokość stożka. Przekrój ten jest trójkątem równoramiennym. Na poniższym rysunku przekrój ten został oznaczony na niebiesko. Kąt α nazywany jest kątem rozwarcia stożka.
Dla stożka o promieniu podstawy r i wysokości h oraz tworzącej l przekrój osiowy jest trójkątem o bokach 2r,l,l . Pole przekroju osiowego jest równe iloczynowi promienia razy wysokość stożka co wyraża wzór:

Przekrój osiowy stożka jest trójkątem równobocznym
W tym przypadku długości boków trójkąta będą równe średnicy podstawy stożka czyli 2r. W takim przypadku wysokość stożka będzie równa r √ 3. Stąd pole powierzchni przekroju osiowego będzie równe : P=r * h = r * r √ 3 = r2 √ 3.Przekrój osiowy stożka jest trójkątem prostokątnym
W takim przypadku wysokość trójkąta będzie równa promieniowi r podstawy stożka. Stąd pole przekroju osiowego będzie równe: P = r * h = r2.Przekrój osiowy stożka - zadania
Zadanie 1Dany jest stożek o r=4 i h=3. Oblicz pole przekroju osiowego.
Rozwiązanie
P=r * h=4*3=12
Zadanie 2
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 6. Oblicz objętość stożka.
Rozwiązanie
Promień podstawy stożka, o którym mowa w zadaniu wynosi 3. Wyznaczmy wysokość stożka:

Znając teraz wysokość liczymy objętość stożka:
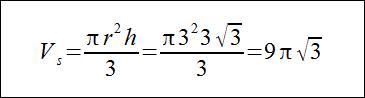
Zadanie 3
Przekrój osiowy stożka jest trójkątem prostokątnym o polu 2. Oblicz pole powierzchni bocznej stożka.
Rozwiązanie
Przekrój osiowy stożka obrotowego jest trójkątem równoramiennym. Jeśli jeden z jego kątów ma miarę 90 stopni to może to być tylko kąt rozwarcia. W zadaniu mamy zatem do czynienia z trójkątem o kątach 45,45,90. Pole takiego trójkąta będzie równe (l to długość tworzącej stożka) :

Obliczmy promień stożka. Przekrój osiowy jest trójkątem 90,45,45 co oznacza, że promień stożka będzie równy połowie przeciwprostokątnej tego trójkąta:
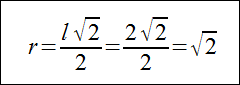
Teraz już możemy obliczyć pole powierzchni bocznej stożka:

Zadanie 4
Kąt rozwarcia stożka wynosi 120°. Oblicz pole przekroju osiowego tego stożka jeśli jego objętość jest równa (100 pi * √3 )/3.
Rozwiązanie
Jeśli kąt rozwarcia stożka jest równy 120° to tworząca, wysokość i promień podstawy tworzą trójkąt 30,60,90. Stąd otrzymujemy związek między h i r:
h/r = tg 30 °
Dodatkowo znając objętość możemy napisać równanie:
(100 pi * √3 )/3 = pi * r2 * h/3
Stąd otrzymujemy:

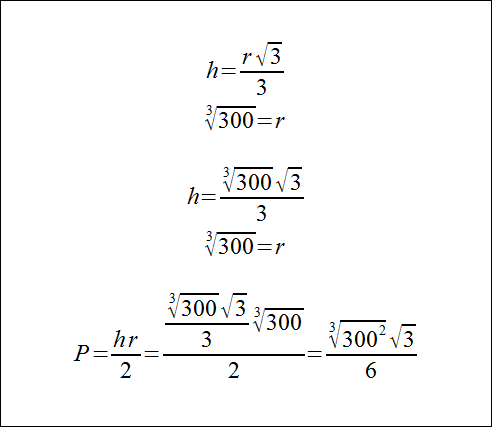
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (3)
2013-03-24 18:48:24 Ania napisał(a):
Witam mam problem z zadaniem o treści:
W kulę wpisano stożek którego przekrojem osiowym jest trójkąt równoboczny o boku długości a=6cm. Oblicz objętość kuli i stożka.
Proszę o szybkie rozwiązanie zadanie potrzebne na wtorek :)
2013-03-24 20:00:13 ania napisał(a):
mam również problem z paroma innymi zadaniami i proszę o pomoc
2) w ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a=5cm. krawędź boczna ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 60 stopni. oblicz objętość i pole powierzchni całkowitej ostrosłupa
3) przekątna przekroju osiowego walca jest nachylona do wysokości pod kątem 30 stopni oblicz pole powierzchni walca i objętość jeżeli jego wysokość ma 8cm
2013-03-25 19:22:05 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie zadania:
Pozdrawiam
Marcin - BazyWiedzy.COM
