Strona główna > Matematyka > Geometria przestrzenna > Objętość graniastosłupa

Gdzie:
V - objętość graniastosłupa
Pp- pole podstawy graniastosłupa
h- wysokość graniastosłupa
W podanych poniżej wzorach a jest długością krawędzi podstawy, h - wysokością graniastosłupa.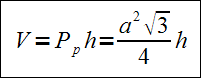
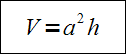

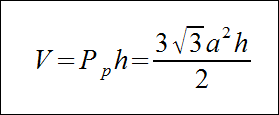
W graniastosłupie prawidłowym trójkątnym krawędź podstawy a ma długość 3. Przekątna ściany bocznej c ma długość 5. Oblicz objętość tego graniastosłupa.

Rozwiązanie
Przekątna ściany bocznej, krawędź podstawy i wysokość graniastosłupa tworzą trójkąt prostokątny. Znając długość krawędzi podstawy i długość przekątnej ściany bocznej możemy (stosując twierdzenie Pitagorasa) obliczyć wysokość graniastosłupa:

2012-06-12 23:16:34 napisał(a):
Dziękuję
2012-06-12 23:17:32 napisał(a):
Ha ha ha nic tu nie ma na poziomie podstawowym i nie można się rozczytać.
2013-02-03 17:13:07 Ryszard S. napisał(a):
Ciągle szukam wzoru na obliczenie objętości wiadra gdzie dno i równoległy otwór górny mają różne powierzchnie. Szukam także wzoru na obliczenie objętości sześcianu gdzie cztery ściany są trapezami a dwie równoległe są różnymi prostokątami. Coś na kształt wiadra "kwadratowego" gdzie boczne ściany są trapezami.
2013-02-03 21:34:26 BazyWiedzy.COM napisał(a):
Witaj Ryszard.
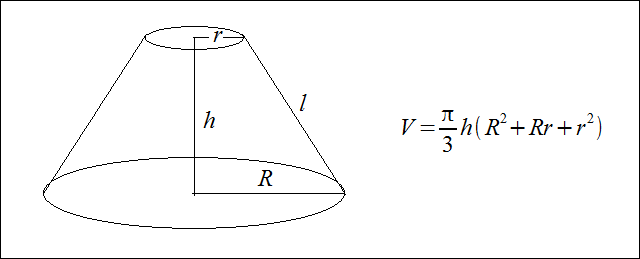
Jeśli chodzi o objętość opisywanego przez Ciebie wiadra to z punktu widzenia matematyki jest to objętość stożka ściętego. Wzór wraz z rysunkiem znajduje się poniżej. Jeśli chodzi o ten drugi wzór to z Twojego opisu wynika, że chodzi Ci o ścięty ostrosłup. Wkrótce umieścimy wzór na objętość ostrosłupa ściętego.
Pozdrawiamy
Zespół BazyWiedzy.COM
2013-02-06 23:36:45 BazyWiedzy.COM napisał(a):
Witaj Ryszard.
Podaję wzór wraz z rysunkiem dla drugiej bryły, o której pisałeś. Nie jest to chyba jednak ostrosłup ścięty. W ostrosłupie ściętym (gdy płaszczyzna cięcia i płaszczyzna podstawy są równoległe) dolna i górna podstawa są prostokątami dla których stosunek odpowiednich boków jest taki sam. Podany wzór jest bardziej ogólny - tzn. nie musi być spełniony warunek a/b=c/d. Jeśli ktoś jest chętny to proszę o wyprowadzenie wzoru i sprawdzenie mojego wzoru.
Pozdrawiam

2013-02-07 22:47:06 BazyWiedzy.COM napisał(a):
Witajcie.
Co do poprzedniego wzoru to znalazłem dwie jego właściwości przemawiające za jego poprawnością. Po pierwsze zauważcie, że gdy c=0 oraz d=0, to wzór powinien stać się wzorem na objętość ostrosłupa. Jest tak rzeczywiście:
V=1/6 * h * ( cb+ad+2ab+2cd)=1/6 * h * ( 0*b+a * 0+2ab+2* 0 *0)=1/6 * h * 2ab=1/3 h * a*b
Po drugie dla c=a i d=b wzór powinien stać się wzorem na objętość graniastosłupa. Sprawdźmy to:
V=1/6 * h * ( cb+ad+2ab+2cd)= 1/6 * h * ( ab+ab+2ab+2ab)=1/6 * h * 6ab=h*a*b
Pozdrawiam
Marcin
BazyWiedzy.COM
2013-03-04 18:03:32 SimonPumba napisał(a):
Dzieki przydało sie :D
2013-03-21 17:36:31 Inna . . *.* napisał(a):
Hej. ,*.* Nie żebym się czepiała ale czy po między V=Pp*H czy ma być V=P pH BO JA JUŻ SAMA NIE WIEM . . .? ? -Będę wdzięczna za odpowiedz ^^ czy w ogóle po między ma być razy . . !!??
2013-03-21 18:06:05 BazyWiedzy.COM napisał(a):
Witaj.
Znak mnożenia czasem można pominąć. We wzorze V=Pp H ,Pp - oznacza pole podstawy (drugie p to indeks dolny - czyli te dwie litery oznaczają jedną wartość), H - to wysokość. Wzór ten można zapisać jako V=Pp*H i to jest to samo.
Pozdrawiam
Marcin - BazyWiedzy.COM
Objętość graniastosłupa
Objętość graniastosłupa jest równa iloczynowi pola podstawy razy wysokość:
Gdzie:
V - objętość graniastosłupa
Pp- pole podstawy graniastosłupa
h- wysokość graniastosłupa
W podanych poniżej wzorach a jest długością krawędzi podstawy, h - wysokością graniastosłupa.
Graniastosłup prawidłowy trójkątny - wzór na objętość
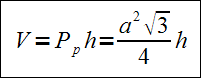
Graniastosłup prawidłowy czworokątny - wzór na objętość
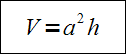
Graniastosłup prawidłowy pięciokątny - wzór na objętość

Graniastosłup prawidłowy sześciokątny - wzór na objętość
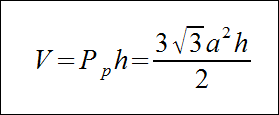
Przykładowe zadania
Zadanie 1W graniastosłupie prawidłowym trójkątnym krawędź podstawy a ma długość 3. Przekątna ściany bocznej c ma długość 5. Oblicz objętość tego graniastosłupa.

Rozwiązanie
Przekątna ściany bocznej, krawędź podstawy i wysokość graniastosłupa tworzą trójkąt prostokątny. Znając długość krawędzi podstawy i długość przekątnej ściany bocznej możemy (stosując twierdzenie Pitagorasa) obliczyć wysokość graniastosłupa:

Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (9)
2012-06-12 23:16:34 napisał(a):
Dziękuję
2012-06-12 23:17:32 napisał(a):
Ha ha ha nic tu nie ma na poziomie podstawowym i nie można się rozczytać.
2013-02-03 17:13:07 Ryszard S. napisał(a):
Ciągle szukam wzoru na obliczenie objętości wiadra gdzie dno i równoległy otwór górny mają różne powierzchnie. Szukam także wzoru na obliczenie objętości sześcianu gdzie cztery ściany są trapezami a dwie równoległe są różnymi prostokątami. Coś na kształt wiadra "kwadratowego" gdzie boczne ściany są trapezami.
2013-02-03 21:34:26 BazyWiedzy.COM napisał(a):
Witaj Ryszard.
Jeśli chodzi o objętość opisywanego przez Ciebie wiadra to z punktu widzenia matematyki jest to objętość stożka ściętego. Wzór wraz z rysunkiem znajduje się poniżej. Jeśli chodzi o ten drugi wzór to z Twojego opisu wynika, że chodzi Ci o ścięty ostrosłup. Wkrótce umieścimy wzór na objętość ostrosłupa ściętego.
Pozdrawiamy
Zespół BazyWiedzy.COM

2013-02-06 23:36:45 BazyWiedzy.COM napisał(a):
Witaj Ryszard.
Podaję wzór wraz z rysunkiem dla drugiej bryły, o której pisałeś. Nie jest to chyba jednak ostrosłup ścięty. W ostrosłupie ściętym (gdy płaszczyzna cięcia i płaszczyzna podstawy są równoległe) dolna i górna podstawa są prostokątami dla których stosunek odpowiednich boków jest taki sam. Podany wzór jest bardziej ogólny - tzn. nie musi być spełniony warunek a/b=c/d. Jeśli ktoś jest chętny to proszę o wyprowadzenie wzoru i sprawdzenie mojego wzoru.
Pozdrawiam

2013-02-07 22:47:06 BazyWiedzy.COM napisał(a):
Witajcie.
Co do poprzedniego wzoru to znalazłem dwie jego właściwości przemawiające za jego poprawnością. Po pierwsze zauważcie, że gdy c=0 oraz d=0, to wzór powinien stać się wzorem na objętość ostrosłupa. Jest tak rzeczywiście:
V=1/6 * h * ( cb+ad+2ab+2cd)=1/6 * h * ( 0*b+a * 0+2ab+2* 0 *0)=1/6 * h * 2ab=1/3 h * a*b
Po drugie dla c=a i d=b wzór powinien stać się wzorem na objętość graniastosłupa. Sprawdźmy to:
V=1/6 * h * ( cb+ad+2ab+2cd)= 1/6 * h * ( ab+ab+2ab+2ab)=1/6 * h * 6ab=h*a*b
Pozdrawiam
Marcin
BazyWiedzy.COM
2013-03-04 18:03:32 SimonPumba napisał(a):
Dzieki przydało sie :D
2013-03-21 17:36:31 Inna . . *.* napisał(a):
Hej. ,*.* Nie żebym się czepiała ale czy po między V=Pp*H czy ma być V=P pH BO JA JUŻ SAMA NIE WIEM . . .? ? -Będę wdzięczna za odpowiedz ^^ czy w ogóle po między ma być razy . . !!??
2013-03-21 18:06:05 BazyWiedzy.COM napisał(a):
Witaj.
Znak mnożenia czasem można pominąć. We wzorze V=Pp H ,Pp - oznacza pole podstawy (drugie p to indeks dolny - czyli te dwie litery oznaczają jedną wartość), H - to wysokość. Wzór ten można zapisać jako V=Pp*H i to jest to samo.
Pozdrawiam
Marcin - BazyWiedzy.COM