Strona główna > Matematyka > Funkcje > Granica funkcji
Funkcja f(x) ma w punkcie x0 granicę równą a, jeśli dla każdego cięgu (xn) argumentów funkcji f(x) zbieżnego do x0 o wyrazach różnych od x0, odpowiadający mu ciąg (yn) wartości funkcji jest zbieżny do a. Zapisujemy to za pomocą wzoru:
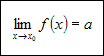
Twierdzenie de l'Hospitala
Jeśli dane są dwie funkcje f(x) i g(x) określone w pewnym otoczeniu punktu x0 i istnieją pochodne f'(x) i g'(x) i zachodzi jeden z warunków:
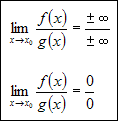
to prawdziwe jest równanie:



Przykłady obliczania granic.
Przykład zastosowania twierdzenia de l'Hospitala

Obliczanie granicy z funkcji wielomianowej - przykład

Obliczanie granicy z funkcji wymiernej - przykład.

2013-01-08 11:22:18 Fremen napisał(a):
Liczenie granicy sin(x)/x za pomocą reguły del Hospitala to "oszustwo" bo do obliczenia wartości pochodnej z licznika, musimy znać szukaną granicę.
Granica funkcji
Definicja granicy funkcjiFunkcja f(x) ma w punkcie x0 granicę równą a, jeśli dla każdego cięgu (xn) argumentów funkcji f(x) zbieżnego do x0 o wyrazach różnych od x0, odpowiadający mu ciąg (yn) wartości funkcji jest zbieżny do a. Zapisujemy to za pomocą wzoru:
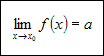
Twierdzenie de l'Hospitala
Jeśli dane są dwie funkcje f(x) i g(x) określone w pewnym otoczeniu punktu x0 i istnieją pochodne f'(x) i g'(x) i zachodzi jeden z warunków:
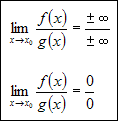
to prawdziwe jest równanie:

Ważne granice funkcji.


Przykłady obliczania granic.
Przykład zastosowania twierdzenia de l'Hospitala

Obliczanie granicy z funkcji wielomianowej - przykład

Obliczanie granicy z funkcji wymiernej - przykład.

Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (1)
2013-01-08 11:22:18 Fremen napisał(a):
Liczenie granicy sin(x)/x za pomocą reguły del Hospitala to "oszustwo" bo do obliczenia wartości pochodnej z licznika, musimy znać szukaną granicę.