Strona główna > Matematyka > Geometria płaszczyzny > Wzór na pole trójkąta

Przekształcanie wzorów Okrąg wpisany w trójkąt
Pole trójkąta jest równe połowie iloczynu długości dowolnego boku i długości wysokości opuszczonej na ten bok.
Uzasadnienie wzoru:
Pole prostokąta cefh jest równe a*h. Pary trójkątów cdg i cgh oraz deg i efg mają identyczne pola. Stąd suma pól trójkątów cdg i deg jest równa sumie pól trójkątów cgh i efg. Są one jednocześnie równe połowie pola prostokąta. Suma pól cdg i deg jest równa szukanemu polu trójkąta ceg. Czyli pole trójkąta ceg jest równe połowie pola prostokąta.
Wyprowadzenie wzoru na pole trójkąta równobocznego

Z twierdzenia Pitagorasa dla trójkąta DBC mamy:

Dany jest trójkąt równoboczny o wysokości h=5. Oblicz jego pole.
Rozwiązanie
Z wzoru na wysokość obliczamy a:
h=a*pierwiastekz(3)/2
5=a*pierwiastekz(3)/2 | *2
10=a*pierwiastekz(3)
10/pierwiastekz(3)=a
Następnie korzystamy z wzoru na pole trójkąta:
P=a2pierwiastekz(3)/4=(10/pierwiastekz(3))2pierwiastekz(3)/4
P=100/3 * pierwiastekz(3)/4 = 25 * pierwiastekz(3)/3
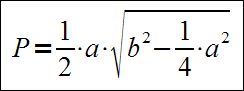
2012-06-11 19:19:00 bili napisał(a):
jest to nudne ello
Wzór na pole trójkąta

Przekształcanie wzorów Okrąg wpisany w trójkąt
Pole trójkąta jest równe połowie iloczynu długości dowolnego boku i długości wysokości opuszczonej na ten bok.
Uzasadnienie wzoru:
Pole prostokąta cefh jest równe a*h. Pary trójkątów cdg i cgh oraz deg i efg mają identyczne pola. Stąd suma pól trójkątów cdg i deg jest równa sumie pól trójkątów cgh i efg. Są one jednocześnie równe połowie pola prostokąta. Suma pól cdg i deg jest równa szukanemu polu trójkąta ceg. Czyli pole trójkąta ceg jest równe połowie pola prostokąta.
Wyprowadzenie wzoru na pole trójkąta równobocznego

Z twierdzenia Pitagorasa dla trójkąta DBC mamy:

Pole trójkąta - przykładowe zadania
Zadanie 1Dany jest trójkąt równoboczny o wysokości h=5. Oblicz jego pole.
Rozwiązanie
Z wzoru na wysokość obliczamy a:
h=a*pierwiastekz(3)/2
5=a*pierwiastekz(3)/2 | *2
10=a*pierwiastekz(3)
10/pierwiastekz(3)=a
Następnie korzystamy z wzoru na pole trójkąta:
P=a2pierwiastekz(3)/4=(10/pierwiastekz(3))2pierwiastekz(3)/4
P=100/3 * pierwiastekz(3)/4 = 25 * pierwiastekz(3)/3
Pole trójkąta równoramiennego
Dla trójkąta równoramiennego o podstawie a i ramionach b mamy pole dane wzorem: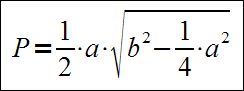
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (1)
2012-06-11 19:19:00 bili napisał(a):
jest to nudne ello