Strona główna > Matematyka > Geometria płaszczyzny > Trójkąt równoramienny


Korzystając z twierdzenia Pitagorasa i z faktu, że wysokość trójkąta równoramiennego dzieli podstawę na 2 połowy możemy wyznaczyć wzór na pole trójkąta równoramiennego w zależności od boków a,b:

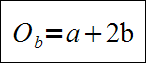

Aby wyznaczyć pozostałe dwie wysokości (opuszczone na ramiona b) skorzystamy z wzoru na pole trójkąta:


Następnie rozwartością cyrkla równą długości ramienia trójkąta rysujemy odpowiednie łuki (tak jak to pokazano na rysunku).

Punkt przecięcia łuków to trzeci (szukany) wierzchołek trójkąta równoramiennego. Łączymy następnie punkt przecięcia łuków z końcami odcinka będącego podstawą trójkąta.


2013-02-25 21:08:10 lila napisał(a):
oblicz pole trojkata równoramiennego mając obw=12 i wys.2 pierwiastki z 3. jak to zrobić?
2013-02-25 23:21:49 BazyWiedzy.COM napisał(a):
Witaj Lila.
Oto rozwiązanie zadania:
Pozdrawiam
Marcin - BazyWiedzy.COM

2013-02-26 22:36:33 lila napisał(a):
dzieki za pomoc :)
2013-02-26 23:22:48 BazyWiedzy.COM napisał(a):
Cieszę się, że pomoc się przydała ;-) Pozdrawiam.
2013-02-27 18:27:38 Lukas napisał(a):
W trójkącie równoramiennym poprowadzono dwusieczną kąta przy podstawie, która podzieliła ramię na dwa odcinki długości 4 cm i 6 cm. Oblicz długość podstawy tego trójkąta. Rozpatrz dwa przypadki. Proszę o pomoc
2013-03-09 18:47:14 Black napisał(a):
Trójkąta równoramiennego nie można zbudować z odcinków o długościach a 13,13,17cm b 21,17,21cm c 65,35,35 d 19,38,19 plis szybko
2013-03-09 20:04:17 BazyWiedzy.COM napisał(a):
Witaj.
Aby można było zbudować trójkąt równoramienny z odcinków o podanych długościach to suma długości jednakowych ramion musi być większa od długości trzeciego ramienia. Z podanych trójek tylko ostatnia nie spełnia tego warunku (suma jest równa a powinna być większa):
19+19=38
Zatem z trójki 19,38,19 nie można zbudować trójkąta równoramiennego.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-10 18:14:30 Black napisał(a):
Dziękuję za odpowiedź.
2013-03-20 20:56:11 anna napisał(a):
Zadanie zamknięte:
1.Dany jest trójkąt równoramienny o obwodzie 14.Stosunek ramienia trójkąta do jego podstawy jest równy 3:2.Podstawa tego trójkąta ma długość:
a)6
b)5 i 1/4
c)4
d)3 i 1/2
2013-04-13 17:51:07 BazyWiedzy.COM napisał(a):
Oto rozwiązanie:
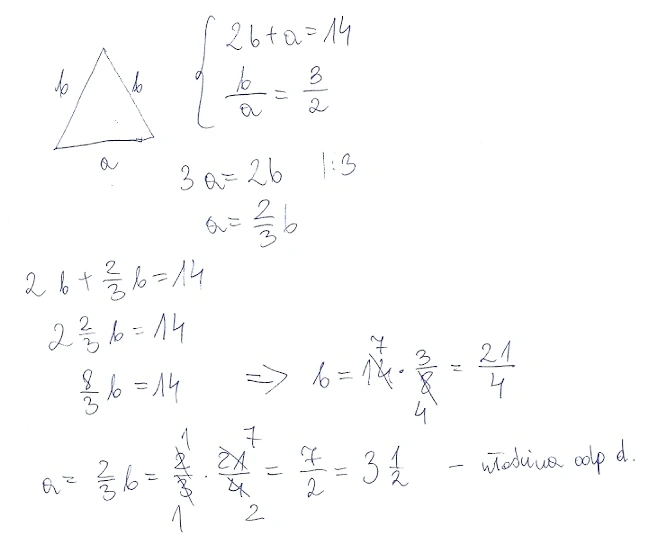
2013-04-13 17:51:08 Danio :) napisał(a):
Pole trójkąta równoramiennego wynosi 3 pierwiastki z 3 cm . Podstawa tworzy z ramieniem kąt 30 stopni . Oblicz długość podstawy tego trójkąta . MOŻECIE WYTŁUMACZYĆ MI TO ZADANIE ????
2013-04-13 18:20:11 BazyWiedzy.COM napisał(a):
Oto rozwiązanie i wyjaśnienie zadania:

2013-05-15 16:39:06 xxx napisał(a):
Liczby 4,10,c są długościami boków trójkąta równoramiennego. Oblicz c.
2013-05-15 19:32:46 BazyWiedzy.COM napisał(a):
Aby dany trójkąt był równoramienny długości dwóch boków muszą być identyczne: czyli mamy do wyboru 4,10,10 lub 4,10,4. Opcja 4,10,4 odpada dlatego, że 4+4<10 - nie uda się z tych odcinków zbudować trójkąta. Tak więc prawidłowa odpowiedź to:4,10,10.
Pozdrawiam - Marcin
2013-05-19 17:22:59 Kaka napisał(a):
Informacje przydały się :D .
2013-05-28 20:49:52 lol napisał(a):
podstawa w tr. równoramiennym ma 8cm a promień wpisany 2cm. ile wynosi pole ?
2015-09-07 21:22:50 Wojownik napisał(a):
W trójkącie równoramiennym ABC o podstawie AB kąt między ramionami ma miarę 40 stopni, a dwusieczne kątów przy podstawie przecinają się w punkcie D. Oblicz miarę kąta ADB. Jak to zrobić? Proszę o pośpiech.
2015-09-07 23:38:33 BazyWiedzy.COM napisał(a):
Witaj. Oto rozwiązanie. Pozdrawiam
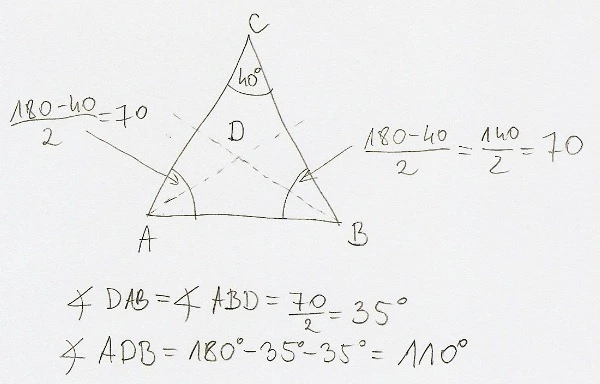
2016-01-02 20:24:48 Dominika napisał(a):
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 6. Wysokość tego trójkąta opuszczana na ramię wynosi 4 pierwiastki z 2. Jak obliczyć długość wysokości poprowadzonej na podstawę?
2016-01-03 17:23:22 Agnieszka napisał(a):
Jak obliczyć bok w trojkącie rownoramiennym znajac jego wysokosc i podstawe?
2016-06-21 13:27:30 napisał(a):
Jestem expertem i niektóre rzeczy mi się nie podobają
2023-07-20 18:13:15 Zbigniew napisał(a):
Dzień Dobry! Czy można obliczyć boki trójkąta równoramiennego jeśli dane są tylko wartości kątów? Wdzięczny z życzliwych odpowiedzi, Zbigniew
Trójkąt równoramienny
Trójkąt równoramienny to taki trójkąt, w którym dwa boki mają jednakową długość. W trójkącie równoramiennym kąty przy podstawie mają taką samą miarę. Wysokość opuszczona na podstawę trójkąta równoramiennego dzieli ją na dwa równe odcinki. Oznacza to, że wysokość zawiera w sobie symetralną podstawy. Wysokość opuszczona na podstawę trójkąta zawiera w sobie dwusieczną odpowiedniego kąta. Na poniższym rysunku przedstawiono trójkąt równoramienny o bokach a,b,b i wysokości h:
Kąty w trójkącie równoramiennym
Kąty trójkąta równoramiennego, których jednym z ramion jest podstawa tego trójkąta mają równe miary. Jeśli oznaczymy je jako α to trzeci kąt będzie miał miarę: β = 180 - 2α . Korzystamy tu z tego, że suma miar kątów w trójkącie jest zawsze równa 180.Pole trójkąta równoramiennego
Pole trójkąta równoramiennego jest dane wzorem:
Korzystając z twierdzenia Pitagorasa i z faktu, że wysokość trójkąta równoramiennego dzieli podstawę na 2 połowy możemy wyznaczyć wzór na pole trójkąta równoramiennego w zależności od boków a,b:

Obwód trójkąta równoramiennego
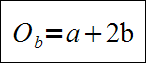
Wysokości trójkąta równoramiennego
Wysokość opuszczona na podstawę a została już wcześniej wyznaczona. Przypomnijmy jeszcze raz wzór na tą wysokość:
Aby wyznaczyć pozostałe dwie wysokości (opuszczone na ramiona b) skorzystamy z wzoru na pole trójkąta:

Konstrukcja trójkąta równoramiennego
Aby skonstruować trójkąt równoramienny musimy najpierw narysować odcinek będący podstawą trójkąta.
Następnie rozwartością cyrkla równą długości ramienia trójkąta rysujemy odpowiednie łuki (tak jak to pokazano na rysunku).

Punkt przecięcia łuków to trzeci (szukany) wierzchołek trójkąta równoramiennego. Łączymy następnie punkt przecięcia łuków z końcami odcinka będącego podstawą trójkąta.

Okrąg wpisany w trójkąt równoramienny
Jeśli okrąg jest wpisany w trójkąt równoramienny o podstawie a i ramionach b to długość promienia tego okręgu jest następująca:
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (22)
2013-02-25 21:08:10 lila napisał(a):
oblicz pole trojkata równoramiennego mając obw=12 i wys.2 pierwiastki z 3. jak to zrobić?
2013-02-25 23:21:49 BazyWiedzy.COM napisał(a):
Witaj Lila.
Oto rozwiązanie zadania:
Pozdrawiam
Marcin - BazyWiedzy.COM

2013-02-26 22:36:33 lila napisał(a):
dzieki za pomoc :)
2013-02-26 23:22:48 BazyWiedzy.COM napisał(a):
Cieszę się, że pomoc się przydała ;-) Pozdrawiam.
2013-02-27 18:27:38 Lukas napisał(a):
W trójkącie równoramiennym poprowadzono dwusieczną kąta przy podstawie, która podzieliła ramię na dwa odcinki długości 4 cm i 6 cm. Oblicz długość podstawy tego trójkąta. Rozpatrz dwa przypadki. Proszę o pomoc
2013-03-09 18:47:14 Black napisał(a):
Trójkąta równoramiennego nie można zbudować z odcinków o długościach a 13,13,17cm b 21,17,21cm c 65,35,35 d 19,38,19 plis szybko
2013-03-09 20:04:17 BazyWiedzy.COM napisał(a):
Witaj.
Aby można było zbudować trójkąt równoramienny z odcinków o podanych długościach to suma długości jednakowych ramion musi być większa od długości trzeciego ramienia. Z podanych trójek tylko ostatnia nie spełnia tego warunku (suma jest równa a powinna być większa):
19+19=38
Zatem z trójki 19,38,19 nie można zbudować trójkąta równoramiennego.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-10 18:14:30 Black napisał(a):
Dziękuję za odpowiedź.
2013-03-20 20:56:11 anna napisał(a):
Zadanie zamknięte:
1.Dany jest trójkąt równoramienny o obwodzie 14.Stosunek ramienia trójkąta do jego podstawy jest równy 3:2.Podstawa tego trójkąta ma długość:
a)6
b)5 i 1/4
c)4
d)3 i 1/2
2013-04-13 17:51:07 BazyWiedzy.COM napisał(a):
Oto rozwiązanie:
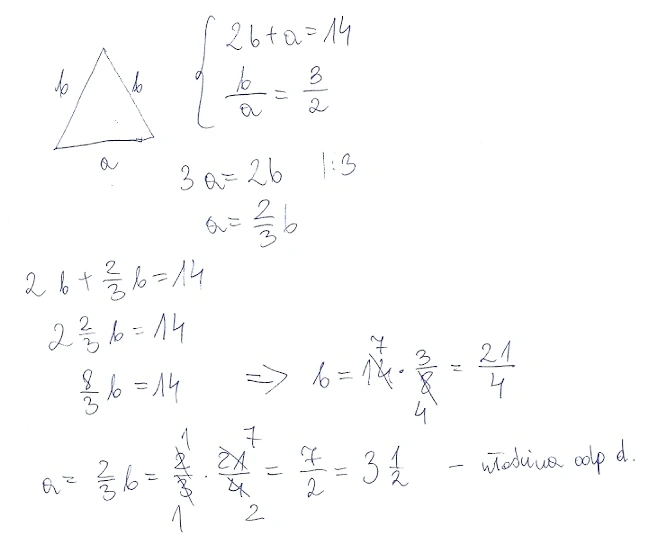
2013-04-13 17:51:08 Danio :) napisał(a):
Pole trójkąta równoramiennego wynosi 3 pierwiastki z 3 cm . Podstawa tworzy z ramieniem kąt 30 stopni . Oblicz długość podstawy tego trójkąta . MOŻECIE WYTŁUMACZYĆ MI TO ZADANIE ????
2013-04-13 18:20:11 BazyWiedzy.COM napisał(a):
Oto rozwiązanie i wyjaśnienie zadania:

2013-05-15 16:39:06 xxx napisał(a):
Liczby 4,10,c są długościami boków trójkąta równoramiennego. Oblicz c.
2013-05-15 19:32:46 BazyWiedzy.COM napisał(a):
Aby dany trójkąt był równoramienny długości dwóch boków muszą być identyczne: czyli mamy do wyboru 4,10,10 lub 4,10,4. Opcja 4,10,4 odpada dlatego, że 4+4<10 - nie uda się z tych odcinków zbudować trójkąta. Tak więc prawidłowa odpowiedź to:4,10,10.
Pozdrawiam - Marcin
2013-05-19 17:22:59 Kaka napisał(a):
Informacje przydały się :D .
2013-05-28 20:49:52 lol napisał(a):
podstawa w tr. równoramiennym ma 8cm a promień wpisany 2cm. ile wynosi pole ?
2015-09-07 21:22:50 Wojownik napisał(a):
W trójkącie równoramiennym ABC o podstawie AB kąt między ramionami ma miarę 40 stopni, a dwusieczne kątów przy podstawie przecinają się w punkcie D. Oblicz miarę kąta ADB. Jak to zrobić? Proszę o pośpiech.
2015-09-07 23:38:33 BazyWiedzy.COM napisał(a):
Witaj. Oto rozwiązanie. Pozdrawiam
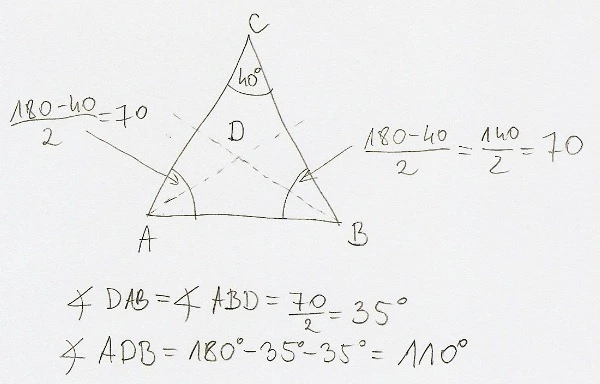
2016-01-02 20:24:48 Dominika napisał(a):
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 6. Wysokość tego trójkąta opuszczana na ramię wynosi 4 pierwiastki z 2. Jak obliczyć długość wysokości poprowadzonej na podstawę?
2016-01-03 17:23:22 Agnieszka napisał(a):
Jak obliczyć bok w trojkącie rownoramiennym znajac jego wysokosc i podstawe?
2016-06-21 13:27:30 napisał(a):
Jestem expertem i niektóre rzeczy mi się nie podobają
2023-07-20 18:13:15 Zbigniew napisał(a):
Dzień Dobry! Czy można obliczyć boki trójkąta równoramiennego jeśli dane są tylko wartości kątów? Wdzięczny z życzliwych odpowiedzi, Zbigniew