Strona główna > Matematyka > Geometria w układzie xy > Równanie prostej
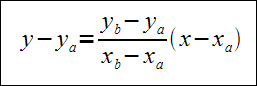
Jeśli prosta przechodzi przez punkt A(xa,ya) to prawdziwe jest równanie ya=axa+b. Równanie to spełnia nieskończenie wiele par współczynników a,b. Oznacza to, że przez dany punkt A przechodzi nieskończenie wiele prostych.
Jeśli prosta przechodzi przez punkt B(xb,yb) to prawdziwe jest równanie yb=axb+b. Równanie to spełnia nieskończenie wiele par współczynników a,b. Oznacza to, że przez dany punkt B przechodzi nieskończenie wiele prostych.
Jeśli A≠B to istnieje dokładnie jedna para a,b taka, że prosta y=ax+b przechodzi przez obydwa punkty A i B. Aby ją wyznaczyć należy rozwiązać układ równań:
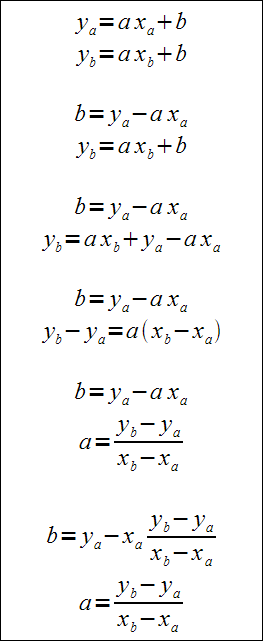
Następnie wstawiamy otrzymaną parę współczynników a,b do równania y=ax+b:
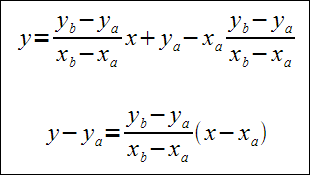
Rozwiązanie
Do wzoru na równanie prostej podstawiamy współrzędne punktów A i B:
y-1=[(-1-1)/(2-1)]*(x-1)
y-1=-2*(x-1)
y=-2x+3
Równanie prostej.
Równanie prostej przechodzącej przez dwa punkty A(xa,ya) i B(xb,yb) jest następujące: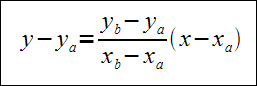
Równanie prostej - wyprowadzenie.
Ogólne równanie prostej ma postać: y=ax+b.Jeśli prosta przechodzi przez punkt A(xa,ya) to prawdziwe jest równanie ya=axa+b. Równanie to spełnia nieskończenie wiele par współczynników a,b. Oznacza to, że przez dany punkt A przechodzi nieskończenie wiele prostych.
Jeśli prosta przechodzi przez punkt B(xb,yb) to prawdziwe jest równanie yb=axb+b. Równanie to spełnia nieskończenie wiele par współczynników a,b. Oznacza to, że przez dany punkt B przechodzi nieskończenie wiele prostych.
Jeśli A≠B to istnieje dokładnie jedna para a,b taka, że prosta y=ax+b przechodzi przez obydwa punkty A i B. Aby ją wyznaczyć należy rozwiązać układ równań:
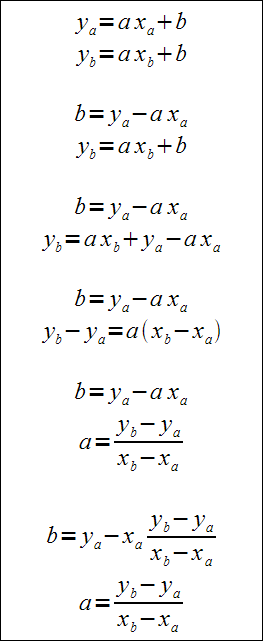
Następnie wstawiamy otrzymaną parę współczynników a,b do równania y=ax+b:
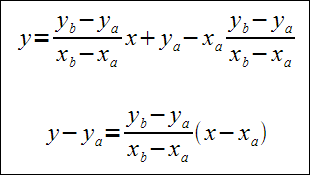
Równanie prostej - przykładowe zadanie
Należy wyznaczyć równanie prostej przechodzącej przez punkty A(1,1) i B(2,-1).Rozwiązanie
Do wzoru na równanie prostej podstawiamy współrzędne punktów A i B:
y-1=[(-1-1)/(2-1)]*(x-1)
y-1=-2*(x-1)
y=-2x+3