Strona główna > Matematyka > Równania i nierówności > Równanie kwadratowe
Wyróżnik trójmianu kwadratowego: Δ=b2-4ac
Jeśli Δ>0 to pierwiastki równania kwadratowego wyrażają się wzorami:
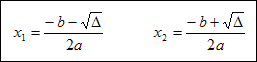
Dla przypadku gdy Δ=0 mamy:
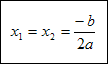
Gdy Δ<0 wówczas równanie nie posiada pierwiastków rzeczywistych.
Przykład: Należy rozwiązać równanie 2x2+12x-14=0.
Rozwiązanie

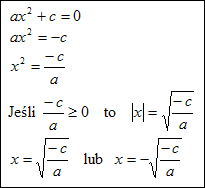
Dla c=0 mamy:
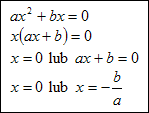
2x2+ax+2=0
w zależności od parametru a.
Rozwiązanie
Wyznaczamy deltę:
Δ = a2-4*2*2=a2-42=(a-4)(a+4)
Równanie ma jedno rozwiązanie gdy:
Δ = 0
(a-4)(a+4)=0
a=-4 lub a=4
Równanie ma dwa rozwiązania gdy:
Δ > 0
a2-16 > 0
a < -4 lub a > 4
Równanie nie posiada rozwiązań w zbiorze R gdy:
a2-16 < 0
a > -4 i a < 4
2012-09-16 19:42:41 Dylluan napisał(a):
Co zrobić jeśli zamiast parametru a,b lub c, musimy obliczyć w zależności od parametru y (w tym wypadku podanego jako 0)?
2012-11-22 21:24:36 Aneta napisał(a):
Może ktoś mógłby pomóc - zadania załączam ..... niestety chociaż bardzo przydatna stronka, tłumaczenie szczegółowe to nie wszystko rozumiem. Liczę na pomoc. Z góry dziękuję
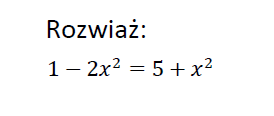
2012-11-22 21:29:29 BazyWiedzy.COM napisał(a):
Przekształcamy równanie:
1-2x2=5+x2
-2x2-x2 -5+1=0
-3x2 -4=0
3x2 +4=0
x2 +4/3=0
Jest to równanie kwadratowe niezupełne, które nie posiada rozwiązań. Można to dodatkowo sprawdzić obliczając deltę:
delta=02-4*1*4/3=-16/3 < 0
2012-12-02 20:03:36 BazyWiedzy.COM napisał(a):
Witaj.
Oto przykład równania, o którym piszesz:
x2+2x+3=y
Porządkujemy równanie:
x2+2x+3-y=0
Obliczamy deltę:
delta=22-4*1*(3-y)=4y-8
Rozpatrujemy 3 przypadki:
delta <0 - brak rozwiązań
y < 2
delta=0 - 1 rozwiązanie
y=2
delta>0 - 2 rozwiązania
y>2
2013-01-23 18:22:51 Mariusz napisał(a):
a jakie jest rozwiązanie równania gdy ax2+bx+c=0 , gdzie a jest mniejsze zera ?? błagam o odpowiedź
2013-01-23 23:08:56 BazyWiedzy.COM napisał(a):
Witaj.
Gdy a < 0 to sposób rozwiązywania równania jest taki sam jak dla a>0. Stosujemy dokładnie takie same wzory: na deltę i na pierwiastki. Jeśli masz problem z jakimś równaniem kwadratowym dodaj je w komentarzu - postaram się pomóc :-)
Pozdrawiam
2013-02-16 09:20:28 Mati napisał(a):
A jak rozwiązać takie zadania ? 5x-3+=2x2 (2x kwadrat)
2013-02-16 19:49:08 BazyWiedzy.COM napisał(a):
Witaj.
5x-3=2x2
Rozwiązujemy to jak zwykłe równanie kwadratowe:
5x-3=2x2
-2x2+5x-3=0
delta=25-4*(-2)*(-3)=25-24=1
pierwiastek z delty=1
x1 = (-5-1)/-4=-6/-4=3/2
x2 = (-5+1)/-4=-4/-4=1
Pozdrawiam
Marcin
2013-02-17 12:56:18 Dagmara napisał(a):
Rozwiązuje te zadania koleżance i za duże liczby mi wychodzą i nie wiem czy dobrze. Pomóżcie ... :D
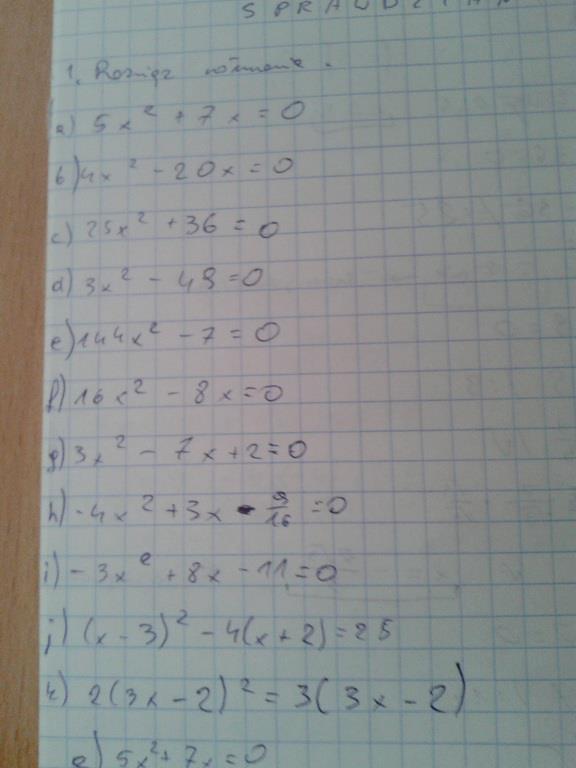
2013-02-17 17:04:41 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązania zadań.
Pozdrawiam
Marcin

2013-03-04 22:22:50 Natucha napisał(a):
Proszę o rozwiązanie tego równania kwadratowego:
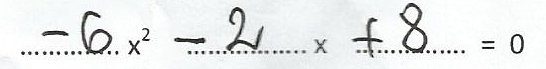
2013-03-04 23:53:23 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie równania:
delta = (-2)2-4*(-6)*8=4+192=196
pierwiastek z delty = 14
x1 = (2-14)/(-12)=1
x2 = (2+14)/(-12)=-16/12=-4/3
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-05 14:57:40 dżastuś napisał(a):
pomocy
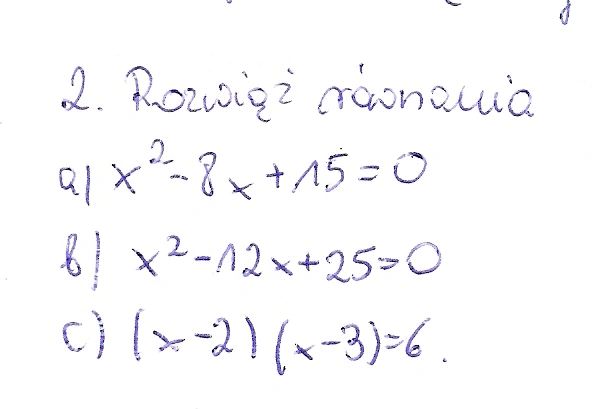
2013-03-05 20:33:51 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązania:
a)
delta=64-4*1*15 = 4
√delta=2
x1=(8-2)/2=6/2=3
x2=(8+2)/2=10/2=5
b)
delta=144-4*1*25 = 44
√delta=2 √11
x1=(12-2√11)/2=6-√11
x2=(12+2√11)/2=6+√11
c)
(x-2)(x-3)=6
x2-3x-2x+6=6
x2-5x+6-6=0
x2-5x=0
x(x-5)=0
x=0 lub x=5
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-04-06 20:11:15 Dorota napisał(a):
proszę o rozwiązanie równania, mnie wychodzi inny wynik niż podany w książce (x+2y)²-(x-2y)², zapomniałam dodać że x=pierwiastek kwadratowy z 2, a y=-pierwiastek kwadratowy z 2
2013-04-06 23:15:13 BazyWiedzy.COM napisał(a):
Witaj.
W podanym przez Ciebie wyrażeniu nie ma znaku równości, a ponadto są tutaj dwie niewiadome. Jeśli możesz to przepisz dokładną treść zadania z książki.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-04-06 23:54:34 Dorota napisał(a):
Wartość liczbowa wyrażenia (x+2y)²-(x-2y)² dla x=pierwiastek kwadratowy z 2, y=- pierwiastek kwadratowy z 2 wynosi: Trzeba obliczyć wartość wyrażenia
2013-04-07 00:59:08 BazyWiedzy.COM napisał(a):
Oto rozwiązanie :
Pozdrawiam
Marcin - BazyWiedzy.COM
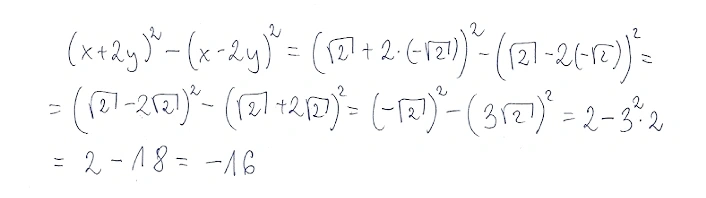
2013-04-07 18:43:00 Dorota napisał(a):
Dziękuję.Mnie wyszło tak samo,a w książce z testami maturalnymi jest wynik =16, a nie -16
2013-04-07 21:08:11 BazyWiedzy.COM napisał(a):
Ja liczyłem to jeszcze innym sposobem i wynik wyszedł taki sam więc w książce jest błąd ;-)
2013-04-08 10:28:42 Dorota napisał(a):
Dzięki za potwierdzenie, też liczyłam na różne sposoby i zawsze mi wychodziło -16, ale potrzebowałam potwierdzenia, że czegoś nie przekręcam.
2013-04-28 18:10:05 dada napisał(a):
Jeżeli 2x-2=^3x+2+2 to jaki będzie wynik?
2013-04-29 09:11:33 katarzynka79 napisał(a):
Błagam o pomoc .dla jakich wartości parametru m równanie mx^2-m(m+1)x+1=0 ma dokładnie jedno rozwiązanie ...pilne Proszę pomóżcie.pozdrawiam
2013-04-29 16:37:58 BazyWiedzy.COM napisał(a):
Oto rozwiązanie:
Pozdrawiam Marcin

2013-04-29 19:18:08 katarzynka79 napisał(a):
Ślicznie dziękuję też wyszło mi, że m=1 ale podstawiłam od razu za m 1 ale .mam jeszcze równanie z wartością bezwzględną czy mogę prosić o pomoc nie mam pojęcia z której strony to ugryźć z góry wielkie DZIĘKUJĘ.|3x-x2|= x2-3x
2013-04-29 20:10:58 BazyWiedzy.COM napisał(a):
Oto rozwiązanie:
Pozdrawiam Marcin
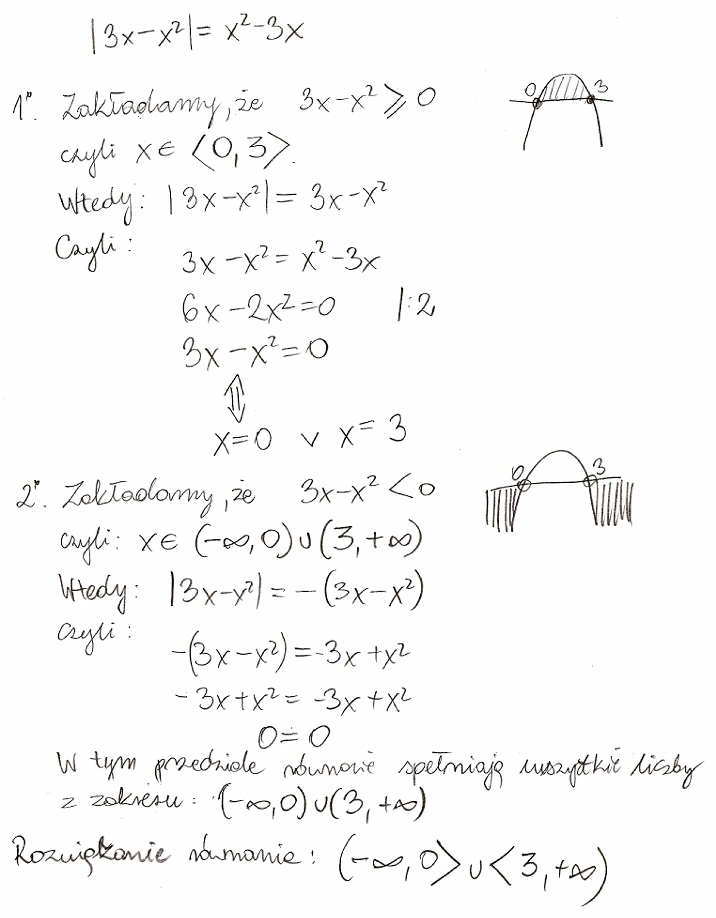
2013-04-29 22:35:33 katarzynka79 napisał(a):
Marcin WIELKIE DZIĘKUJĘ :)pozdrawiam ....mam jeszcze kilka ale nie będę Cię już zamęczać może jakoś sobie poradzę jeśli nie będzie mi szło to się zgłoszę :)
2013-04-29 23:12:08 BazyWiedzy.COM napisał(a):
:-) Nie ma sprawy, jak coś to pisz. Jeśli będę mógł to pomogę. Pamiętaj tylko aby dodawać zadania pod artykułami powiązanymi tematycznie - jak na razie idzie Ci dobrze :-) Pozdrawiam.
Marcin
2013-04-30 09:20:56 katarzynka79 napisał(a):
Witam wiec rozwiązałam i chyba jest dobrze ale będę wdzięczna jak zerkniesz na to swoim fachowym okiem :) wiec |x^2+9|+|x^2+4|=5 wiec zrobiłam to w 3 przypadkach1)-x^2+9-x^2+4=5 -2x^+13=5 -2x^2=-8 x=3 i x=-3 wiec x należy do przedziału (-2,2) .2)-x^2+9+x^2-4=5 x^2-9 < 0 ,x^2-4>lub równe 0 z tego wychodzi ze 5=5 3).x^2-9+x^2-4=5 2x^2=18 x=3 i x=-3 x należy do (-nieskończoność ,-3> suma < 3,+nieskończoność )...takie coś mi wyszło zerknij czy dobrze .pozdrawiam
2013-04-30 23:31:06 BazyWiedzy.COM napisał(a):
Witaj.
Czy pod wartościami bezwzględnymi są na pewno wyrażenia: x2+9 i x2+4 (a nie x2-9 i x2-4) ? Bo jeśli tak to: wyrażenia, te są zawsze dodatnie. W takim przypadku można zwyczajnie opuścić znaki wartości bezwzględnych. W załączniku masz rozwiązanie. Jeśli pod wartościami bezwzględnymi będą minusy to napisz bo oczywiście wtedy rozwiązanie będzie inne.
Pozdrawiam - Marcin

2013-05-01 19:44:32 katarzynka79 napisał(a):
Dzięki masz rację w wartości bezwzględnej są - i wtedy rzeczywiście rozwiązanie będzie inne i skromnie powiem, że chyba tym razem nie zrobiłam błędu...pozdrawiam i życzę miłej i ciepłej majówki :)
2013-05-02 01:29:21 BazyWiedzy.COM napisał(a):
Witaj.
Na wstępie chciałem napisać, że cieszę się, że samodzielnie próbujesz rozwiązać te zadania - niestety często jest tak, że użytkownicy portalu szukają tylko gotowych rozwiązań. Dlatego punkt dla Ciebie :-). Odnośnie Twojego zadania:
Przy rozwiązywaniu równań z wartościami bezwzględnymi trzeba zawsze wyznaczyć miejsca zerowe wyrażeń pod wartością bezwzględną. Te miejsca zerowe dzielą nam wówczas cały zbiór liczb rzeczywistych na podzbiory, w których rozpatrujemy potem równanie. W Twoim przypadku pod wartościami bezwzględnymi są wyrażenia, które mają po dwa miejsca zerowe. W sumie te cztery miejsca zerowe dzielą cały zbiór R na aż 5 przedziałów. W tych przedziałach należy rozpatrzyć całe równanie. W załączniku masz rozwiązanie. Wynik dodatkowo sprawdziłem zupełnie inną metodą. Utworzyłem dwie funkcje: f(x)=|x2 -9|+|x2 -4| oraz g(x)=5. Narysowałem je i sprawdziłem gdzie się pokrywają (to jest rozwiązanie równania) i wynik wyszedł dokładnie taki sam. Życzę Ci także przyjemnego weekendu majowego :-)
PS. Tu masz link do wykresu funkcji f(x)=|x2 -9|+|x2 -4|
Pozdrawiam - Marcin

2013-05-02 14:08:50 katarzynka79 napisał(a):
Dzięki Marcin jesteś WIELKI !!!! Pozdrawiam
2013-05-02 17:23:18 BazyWiedzy.COM napisał(a):
:-) :-)
2013-05-06 07:51:41 katarzynka79 napisał(a):
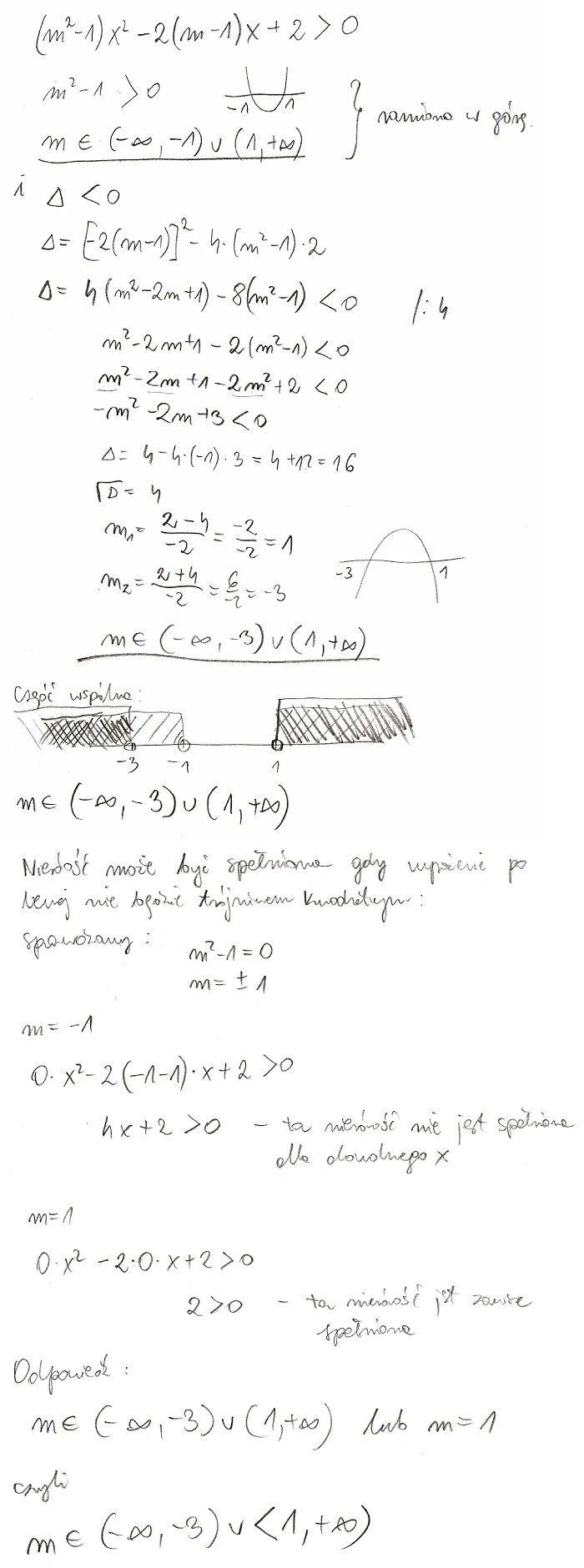
Witam majowy weekend się skończył więc wracamy do rzeczywistości i mam problem z pewnym zadaniem a mianowicie. Dla jakiego m nierówność (m^2-1)x^2-2(m-1)x+2>0 jest prawdziwe dla wszystkich liczb rzeczywistych .Wiec zrobiłam to tak dla m=-1 i wyszło mi tak((-1)-1)x^2-2(-1-1)x+2>0 z tego wynika że x>-1/2 następnie dla m=1 i wychodzi (1^2-1)x^2-2(1-1)x+2>0 z tego wynika ze 2>0 następnie liczę deltę i wychodzi mi ze delta =-4m^2-8m+12 i tutaj poległam nie mam pojęcia co dalej robić ,ogólnie to nie wiem też czy dobrze rozumuje ten parametr m jest dla mnie ciężki do ogarnięcia. Marcin zerknij na to proszę i naprowadź mnie na rozwiązanie..dziękuję ślicznie i pozdrawiam
2013-05-06 16:42:43 BazyWiedzy.COM napisał(a):
Witaj.
Ok - więc naprowadzam :-) Aby podana nierówność była prawdziwa dla dowolnego x to wyrażenie po lewej stronie znaku > musi być zawsze (niezależnie od x) większe od 0. To co jest po lewej stronie to funkcja kwadratowa. Teraz postaraj się odpowiedzieć na pytanie: jak powinien wyglądać wykres tej funkcji aby ta nierówność była spełniona? Tzn. wiadomo, że to jest parabola, ale jak ona powinna wg Ciebie wyglądać aby wartości funkcji kwadratowej zawsze były większe od 0? Odpowiedź na to pytanie jest kluczem do rozwiązania zadania.
Pozdrawiam - Marcin
2013-05-06 19:09:29 katarzynka79 napisał(a):
No wiec parabola przechodzi ma 2 miejsca zerowe 1 i -1 ramionami skierowana w górę a x należy do przedziału (- nieskończoność,-1> suma < 1,+ nieskończoność) tak mi wyszło ale czy jest dobrze to nie mam pojęcia ...ten parametr mnie dobije ..klęska po całości..pozdrawiam
2013-05-07 00:08:01 BazyWiedzy.COM napisał(a):
Hmmm. Może zapomnij na chwilę o tej konkretnej paraboli i tym parametrze ;-) Chodziło mi ogólnie - jeśli mamy nierówność:
ax2+bx+c > 0
to jak powinna wyglądać parabola, której wzór znajduje się po lewej stronie nierówności (chodzi mi jak powinny być skierowane ramiona "w górę" czy "w dół", ile powinno być pierwiastków) aby ta nierówność była zawsze spełniona?
Pozdrawiam - Marcin
2013-05-07 22:20:27 BazyWiedzy.COM napisał(a):
Oto rozwiązanie.
Równanie kwadratowe
Równanie kwadratowe ma postać: ax2+bx+c=0 , gdzie a jest różne od 0.Wyróżnik trójmianu kwadratowego: Δ=b2-4ac
Jeśli Δ>0 to pierwiastki równania kwadratowego wyrażają się wzorami:
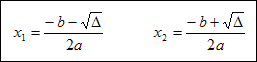
Dla przypadku gdy Δ=0 mamy:
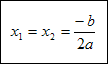
Gdy Δ<0 wówczas równanie nie posiada pierwiastków rzeczywistych.
Przykład: Należy rozwiązać równanie 2x2+12x-14=0.
Rozwiązanie

Równanie kwadratowe niezupełne
Jeśli współczynnik b=0 lub c=0 to wtedy mamy do czynienia z równaniem kwadratowym niezupełnym. Dla b=0 mamy: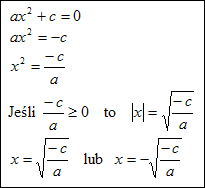
Dla c=0 mamy:
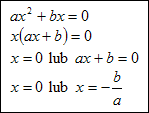
Równanie kwadratowe z parametrem
Należy zbadać ilość rozwiązań równania:2x2+ax+2=0
w zależności od parametru a.
Rozwiązanie
Wyznaczamy deltę:
Δ = a2-4*2*2=a2-42=(a-4)(a+4)
Równanie ma jedno rozwiązanie gdy:
Δ = 0
(a-4)(a+4)=0
a=-4 lub a=4
Równanie ma dwa rozwiązania gdy:
Δ > 0
a2-16 > 0
a < -4 lub a > 4
Równanie nie posiada rozwiązań w zbiorze R gdy:
a2-16 < 0
a > -4 i a < 4
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (39)
2012-09-16 19:42:41 Dylluan napisał(a):
Co zrobić jeśli zamiast parametru a,b lub c, musimy obliczyć w zależności od parametru y (w tym wypadku podanego jako 0)?
2012-11-22 21:24:36 Aneta napisał(a):
Może ktoś mógłby pomóc - zadania załączam ..... niestety chociaż bardzo przydatna stronka, tłumaczenie szczegółowe to nie wszystko rozumiem. Liczę na pomoc. Z góry dziękuję
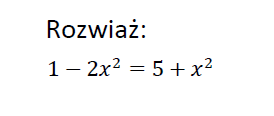
2012-11-22 21:29:29 BazyWiedzy.COM napisał(a):
Przekształcamy równanie:
1-2x2=5+x2
-2x2-x2 -5+1=0
-3x2 -4=0
3x2 +4=0
x2 +4/3=0
Jest to równanie kwadratowe niezupełne, które nie posiada rozwiązań. Można to dodatkowo sprawdzić obliczając deltę:
delta=02-4*1*4/3=-16/3 < 0
2012-12-02 20:03:36 BazyWiedzy.COM napisał(a):
Witaj.
Oto przykład równania, o którym piszesz:
x2+2x+3=y
Porządkujemy równanie:
x2+2x+3-y=0
Obliczamy deltę:
delta=22-4*1*(3-y)=4y-8
Rozpatrujemy 3 przypadki:
delta <0 - brak rozwiązań
y < 2
delta=0 - 1 rozwiązanie
y=2
delta>0 - 2 rozwiązania
y>2
2013-01-23 18:22:51 Mariusz napisał(a):
a jakie jest rozwiązanie równania gdy ax2+bx+c=0 , gdzie a jest mniejsze zera ?? błagam o odpowiedź
2013-01-23 23:08:56 BazyWiedzy.COM napisał(a):
Witaj.
Gdy a < 0 to sposób rozwiązywania równania jest taki sam jak dla a>0. Stosujemy dokładnie takie same wzory: na deltę i na pierwiastki. Jeśli masz problem z jakimś równaniem kwadratowym dodaj je w komentarzu - postaram się pomóc :-)
Pozdrawiam
2013-02-16 09:20:28 Mati napisał(a):
A jak rozwiązać takie zadania ? 5x-3+=2x2 (2x kwadrat)
2013-02-16 19:49:08 BazyWiedzy.COM napisał(a):
Witaj.
5x-3=2x2
Rozwiązujemy to jak zwykłe równanie kwadratowe:
5x-3=2x2
-2x2+5x-3=0
delta=25-4*(-2)*(-3)=25-24=1
pierwiastek z delty=1
x1 = (-5-1)/-4=-6/-4=3/2
x2 = (-5+1)/-4=-4/-4=1
Pozdrawiam
Marcin
2013-02-17 12:56:18 Dagmara napisał(a):
Rozwiązuje te zadania koleżance i za duże liczby mi wychodzą i nie wiem czy dobrze. Pomóżcie ... :D
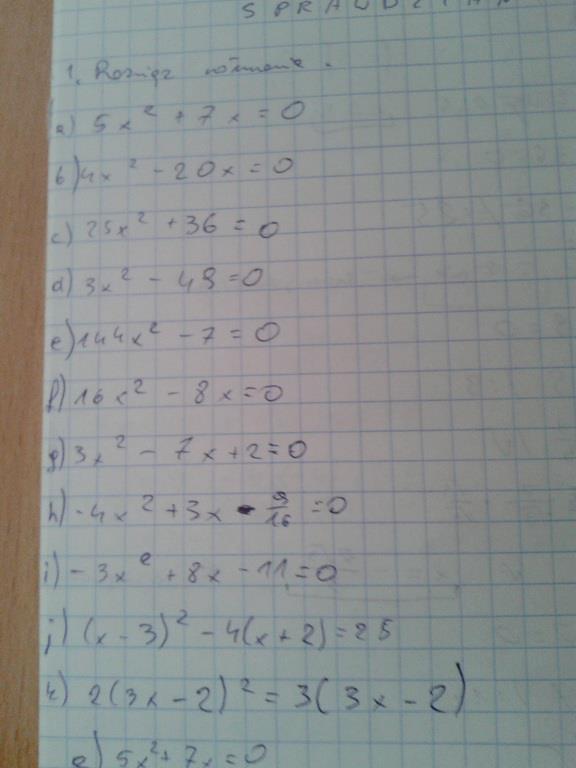
2013-02-17 17:04:41 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązania zadań.
Pozdrawiam
Marcin

2013-03-04 22:22:50 Natucha napisał(a):
Proszę o rozwiązanie tego równania kwadratowego:
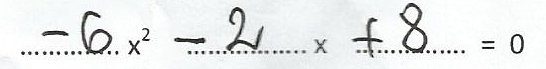
2013-03-04 23:53:23 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie równania:
delta = (-2)2-4*(-6)*8=4+192=196
pierwiastek z delty = 14
x1 = (2-14)/(-12)=1
x2 = (2+14)/(-12)=-16/12=-4/3
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-05 14:57:40 dżastuś napisał(a):
pomocy
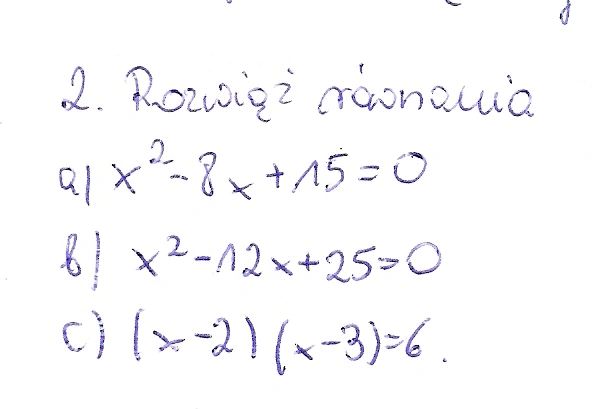
2013-03-05 20:33:51 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązania:
a)
delta=64-4*1*15 = 4
√delta=2
x1=(8-2)/2=6/2=3
x2=(8+2)/2=10/2=5
b)
delta=144-4*1*25 = 44
√delta=2 √11
x1=(12-2√11)/2=6-√11
x2=(12+2√11)/2=6+√11
c)
(x-2)(x-3)=6
x2-3x-2x+6=6
x2-5x+6-6=0
x2-5x=0
x(x-5)=0
x=0 lub x=5
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-04-06 20:11:15 Dorota napisał(a):
proszę o rozwiązanie równania, mnie wychodzi inny wynik niż podany w książce (x+2y)²-(x-2y)², zapomniałam dodać że x=pierwiastek kwadratowy z 2, a y=-pierwiastek kwadratowy z 2
2013-04-06 23:15:13 BazyWiedzy.COM napisał(a):
Witaj.
W podanym przez Ciebie wyrażeniu nie ma znaku równości, a ponadto są tutaj dwie niewiadome. Jeśli możesz to przepisz dokładną treść zadania z książki.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-04-06 23:54:34 Dorota napisał(a):
Wartość liczbowa wyrażenia (x+2y)²-(x-2y)² dla x=pierwiastek kwadratowy z 2, y=- pierwiastek kwadratowy z 2 wynosi: Trzeba obliczyć wartość wyrażenia
2013-04-07 00:59:08 BazyWiedzy.COM napisał(a):
Oto rozwiązanie :
Pozdrawiam
Marcin - BazyWiedzy.COM
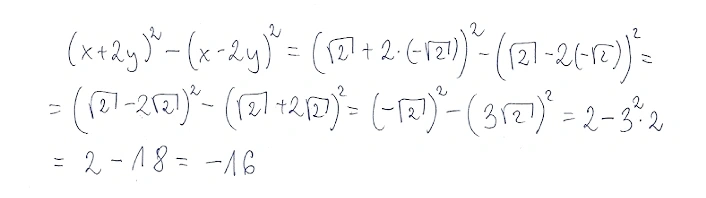
2013-04-07 18:43:00 Dorota napisał(a):
Dziękuję.Mnie wyszło tak samo,a w książce z testami maturalnymi jest wynik =16, a nie -16
2013-04-07 21:08:11 BazyWiedzy.COM napisał(a):
Ja liczyłem to jeszcze innym sposobem i wynik wyszedł taki sam więc w książce jest błąd ;-)
2013-04-08 10:28:42 Dorota napisał(a):
Dzięki za potwierdzenie, też liczyłam na różne sposoby i zawsze mi wychodziło -16, ale potrzebowałam potwierdzenia, że czegoś nie przekręcam.
2013-04-28 18:10:05 dada napisał(a):
Jeżeli 2x-2=^3x+2+2 to jaki będzie wynik?
2013-04-29 09:11:33 katarzynka79 napisał(a):
Błagam o pomoc .dla jakich wartości parametru m równanie mx^2-m(m+1)x+1=0 ma dokładnie jedno rozwiązanie ...pilne Proszę pomóżcie.pozdrawiam
2013-04-29 16:37:58 BazyWiedzy.COM napisał(a):
Oto rozwiązanie:
Pozdrawiam Marcin

2013-04-29 19:18:08 katarzynka79 napisał(a):
Ślicznie dziękuję też wyszło mi, że m=1 ale podstawiłam od razu za m 1 ale .mam jeszcze równanie z wartością bezwzględną czy mogę prosić o pomoc nie mam pojęcia z której strony to ugryźć z góry wielkie DZIĘKUJĘ.|3x-x2|= x2-3x
2013-04-29 20:10:58 BazyWiedzy.COM napisał(a):
Oto rozwiązanie:
Pozdrawiam Marcin
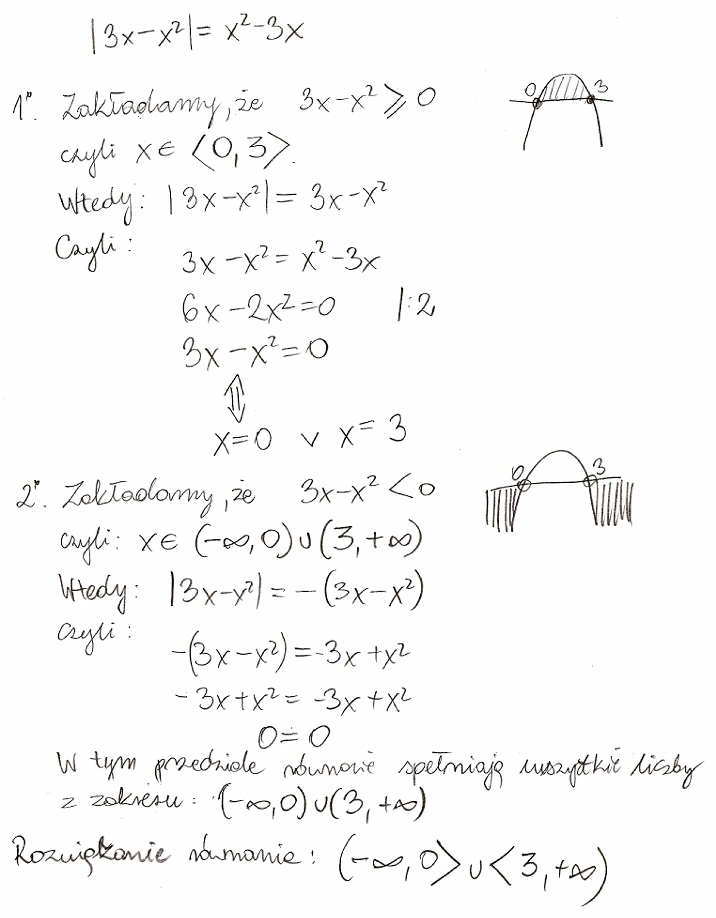
2013-04-29 22:35:33 katarzynka79 napisał(a):
Marcin WIELKIE DZIĘKUJĘ :)pozdrawiam ....mam jeszcze kilka ale nie będę Cię już zamęczać może jakoś sobie poradzę jeśli nie będzie mi szło to się zgłoszę :)
2013-04-29 23:12:08 BazyWiedzy.COM napisał(a):
:-) Nie ma sprawy, jak coś to pisz. Jeśli będę mógł to pomogę. Pamiętaj tylko aby dodawać zadania pod artykułami powiązanymi tematycznie - jak na razie idzie Ci dobrze :-) Pozdrawiam.
Marcin
2013-04-30 09:20:56 katarzynka79 napisał(a):
Witam wiec rozwiązałam i chyba jest dobrze ale będę wdzięczna jak zerkniesz na to swoim fachowym okiem :) wiec |x^2+9|+|x^2+4|=5 wiec zrobiłam to w 3 przypadkach1)-x^2+9-x^2+4=5 -2x^+13=5 -2x^2=-8 x=3 i x=-3 wiec x należy do przedziału (-2,2) .2)-x^2+9+x^2-4=5 x^2-9 < 0 ,x^2-4>lub równe 0 z tego wychodzi ze 5=5 3).x^2-9+x^2-4=5 2x^2=18 x=3 i x=-3 x należy do (-nieskończoność ,-3> suma < 3,+nieskończoność )...takie coś mi wyszło zerknij czy dobrze .pozdrawiam
2013-04-30 23:31:06 BazyWiedzy.COM napisał(a):
Witaj.
Czy pod wartościami bezwzględnymi są na pewno wyrażenia: x2+9 i x2+4 (a nie x2-9 i x2-4) ? Bo jeśli tak to: wyrażenia, te są zawsze dodatnie. W takim przypadku można zwyczajnie opuścić znaki wartości bezwzględnych. W załączniku masz rozwiązanie. Jeśli pod wartościami bezwzględnymi będą minusy to napisz bo oczywiście wtedy rozwiązanie będzie inne.
Pozdrawiam - Marcin

2013-05-01 19:44:32 katarzynka79 napisał(a):
Dzięki masz rację w wartości bezwzględnej są - i wtedy rzeczywiście rozwiązanie będzie inne i skromnie powiem, że chyba tym razem nie zrobiłam błędu...pozdrawiam i życzę miłej i ciepłej majówki :)
2013-05-02 01:29:21 BazyWiedzy.COM napisał(a):
Witaj.
Na wstępie chciałem napisać, że cieszę się, że samodzielnie próbujesz rozwiązać te zadania - niestety często jest tak, że użytkownicy portalu szukają tylko gotowych rozwiązań. Dlatego punkt dla Ciebie :-). Odnośnie Twojego zadania:
Przy rozwiązywaniu równań z wartościami bezwzględnymi trzeba zawsze wyznaczyć miejsca zerowe wyrażeń pod wartością bezwzględną. Te miejsca zerowe dzielą nam wówczas cały zbiór liczb rzeczywistych na podzbiory, w których rozpatrujemy potem równanie. W Twoim przypadku pod wartościami bezwzględnymi są wyrażenia, które mają po dwa miejsca zerowe. W sumie te cztery miejsca zerowe dzielą cały zbiór R na aż 5 przedziałów. W tych przedziałach należy rozpatrzyć całe równanie. W załączniku masz rozwiązanie. Wynik dodatkowo sprawdziłem zupełnie inną metodą. Utworzyłem dwie funkcje: f(x)=|x2 -9|+|x2 -4| oraz g(x)=5. Narysowałem je i sprawdziłem gdzie się pokrywają (to jest rozwiązanie równania) i wynik wyszedł dokładnie taki sam. Życzę Ci także przyjemnego weekendu majowego :-)
PS. Tu masz link do wykresu funkcji f(x)=|x2 -9|+|x2 -4|
Pozdrawiam - Marcin

2013-05-02 14:08:50 katarzynka79 napisał(a):
Dzięki Marcin jesteś WIELKI !!!! Pozdrawiam
2013-05-02 17:23:18 BazyWiedzy.COM napisał(a):
:-) :-)
2013-05-06 07:51:41 katarzynka79 napisał(a):
Witam majowy weekend się skończył więc wracamy do rzeczywistości i mam problem z pewnym zadaniem a mianowicie. Dla jakiego m nierówność (m^2-1)x^2-2(m-1)x+2>0 jest prawdziwe dla wszystkich liczb rzeczywistych .Wiec zrobiłam to tak dla m=-1 i wyszło mi tak((-1)-1)x^2-2(-1-1)x+2>0 z tego wynika że x>-1/2 następnie dla m=1 i wychodzi (1^2-1)x^2-2(1-1)x+2>0 z tego wynika ze 2>0 następnie liczę deltę i wychodzi mi ze delta =-4m^2-8m+12 i tutaj poległam nie mam pojęcia co dalej robić ,ogólnie to nie wiem też czy dobrze rozumuje ten parametr m jest dla mnie ciężki do ogarnięcia. Marcin zerknij na to proszę i naprowadź mnie na rozwiązanie..dziękuję ślicznie i pozdrawiam
2013-05-06 16:42:43 BazyWiedzy.COM napisał(a):
Witaj.
Ok - więc naprowadzam :-) Aby podana nierówność była prawdziwa dla dowolnego x to wyrażenie po lewej stronie znaku > musi być zawsze (niezależnie od x) większe od 0. To co jest po lewej stronie to funkcja kwadratowa. Teraz postaraj się odpowiedzieć na pytanie: jak powinien wyglądać wykres tej funkcji aby ta nierówność była spełniona? Tzn. wiadomo, że to jest parabola, ale jak ona powinna wg Ciebie wyglądać aby wartości funkcji kwadratowej zawsze były większe od 0? Odpowiedź na to pytanie jest kluczem do rozwiązania zadania.
Pozdrawiam - Marcin
2013-05-06 19:09:29 katarzynka79 napisał(a):
No wiec parabola przechodzi ma 2 miejsca zerowe 1 i -1 ramionami skierowana w górę a x należy do przedziału (- nieskończoność,-1> suma < 1,+ nieskończoność) tak mi wyszło ale czy jest dobrze to nie mam pojęcia ...ten parametr mnie dobije ..klęska po całości..pozdrawiam
2013-05-07 00:08:01 BazyWiedzy.COM napisał(a):
Hmmm. Może zapomnij na chwilę o tej konkretnej paraboli i tym parametrze ;-) Chodziło mi ogólnie - jeśli mamy nierówność:
ax2+bx+c > 0
to jak powinna wyglądać parabola, której wzór znajduje się po lewej stronie nierówności (chodzi mi jak powinny być skierowane ramiona "w górę" czy "w dół", ile powinno być pierwiastków) aby ta nierówność była zawsze spełniona?
Pozdrawiam - Marcin
2013-05-07 22:20:27 BazyWiedzy.COM napisał(a):
Oto rozwiązanie.
