Strona główna > Matematyka > Logika > Prawa de Morgana
Zaprzeczeniem koniunkcji dwóch zdań jest alternatywa zaprzeczeń tych zdań. Zapisujemy to symbolicznie:
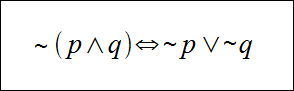
Udowodnijmy podane prawo de Morgana za pomocą tabeli prawdy:

Widzimy, że środkowa i ostatnia kolumna tabeli mają identyczne wartości logiczne, co jest potwierdzeniem I prawa de Morgana.
p ∧ q = "posprzątam pokój i odrobię lekcje"
Aby powyższa koniunkcja była prawdziwa muszę oczywiście wykonać obydwie czynności. Aby była fałszywa - wystarczy, że nie wykonam jednej lub drugiej. Jeśli to zapiszemy:
nie prawda, że (posprzątam pokój i odrobię lekcje) wtedy i tylko wtedy gdy nie posprzątam pokoju lub nie odrobię lekcji
Jeśli zamiast zdań użyjemy symboli p i q wówczas otrzymamy:
~(p ∧ q) ⇔ ~p ∨ ~q
Czyli otrzymaliśmy I prawo de Morgana ;)
II prawo de Morgana
Zaprzeczeniem alternatywy dwóch zdań jest koniunkcja zaprzeczeń tych zdań. Zapisujemy to symbolicznie:
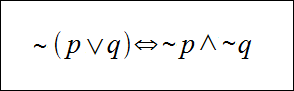
Udowodnijmy podane prawo de Morgana za pomocą tabeli prawdy:

Widzimy, że środkowa i ostatnia kolumna tabeli mają identyczne wartości logiczne, co jest potwierdzeniem II prawa de Morgana.

Co odczytujemy tak:
Nieprawdą jest, że forma zdaniowa Ψ(x) jest prawdziwa dla każdego x należącego do D wtedy i tylko wtedy gdy istnieje takie x należące do D dla, którego forma zdaniowa Ψ(x) nie jest spełniona.
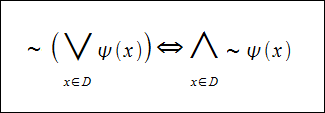
2015-08-19 10:45:57 napisał(a):
Wreszcie zaczęłam cos rozumieć dziękuję! :D
Prawa de Morgana
I prawo de MorganaZaprzeczeniem koniunkcji dwóch zdań jest alternatywa zaprzeczeń tych zdań. Zapisujemy to symbolicznie:
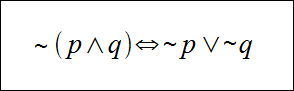
Udowodnijmy podane prawo de Morgana za pomocą tabeli prawdy:

Widzimy, że środkowa i ostatnia kolumna tabeli mają identyczne wartości logiczne, co jest potwierdzeniem I prawa de Morgana.
I prawo de Morgana - przykład z życia
Niech zdanie p="posprzątam pokój" a q="odrobię lekcje". Wówczas koniunkcja p ∧ q będzie równa:p ∧ q = "posprzątam pokój i odrobię lekcje"
Aby powyższa koniunkcja była prawdziwa muszę oczywiście wykonać obydwie czynności. Aby była fałszywa - wystarczy, że nie wykonam jednej lub drugiej. Jeśli to zapiszemy:
nie prawda, że (posprzątam pokój i odrobię lekcje) wtedy i tylko wtedy gdy nie posprzątam pokoju lub nie odrobię lekcji
Jeśli zamiast zdań użyjemy symboli p i q wówczas otrzymamy:
~(p ∧ q) ⇔ ~p ∨ ~q
Czyli otrzymaliśmy I prawo de Morgana ;)
II prawo de Morgana
Zaprzeczeniem alternatywy dwóch zdań jest koniunkcja zaprzeczeń tych zdań. Zapisujemy to symbolicznie:
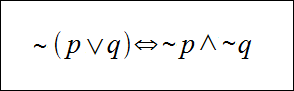
Udowodnijmy podane prawo de Morgana za pomocą tabeli prawdy:

Widzimy, że środkowa i ostatnia kolumna tabeli mają identyczne wartości logiczne, co jest potwierdzeniem II prawa de Morgana.
Prawa de Morgana dla zdań z kwantyfikatorami
Jeśli przez Ψ(x) oznaczymy dowolną formę zdaniową wówczas prawdziwe jest zdanie logiczne:
Co odczytujemy tak:
Nieprawdą jest, że forma zdaniowa Ψ(x) jest prawdziwa dla każdego x należącego do D wtedy i tylko wtedy gdy istnieje takie x należące do D dla, którego forma zdaniowa Ψ(x) nie jest spełniona.
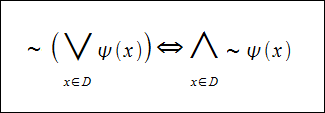
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (1)
2015-08-19 10:45:57 napisał(a):
Wreszcie zaczęłam cos rozumieć dziękuję! :D