Strona główna > Matematyka > Wektory > Iloczyn skalarny wektorów
Iloczyn skalarny dwóch niezerowych wektorów jest równy iloczynowi długości wektorów razy cosinus kąta zawartego między nimi. Wyrażamy to następującym wzorem:
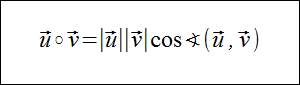
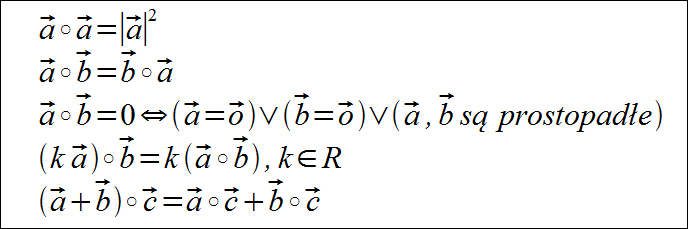
Wyjaśnienia kilku z powyższych wzorów:
Wzór nr 1: Jeśli mamy dwa identyczne wektory to kąt między nimi jest równy 0 °. cos 0 ° = 1 zatem iloczyn skalarny tych wektorów będzie równy iloczynowi ich (identycznych) długości razy 1 czyli będzie równy kwadratowi długości.
Wzór nr 2: Jeśli zmienimy kolejność wektorów przy mnożeniu skalarnym, ich długości się nie zmienią. Zmieni się jedynie kąt między nimi na przeciwny. Jednak jak wiadomo funkcja cosinus jest funkcją parzystą - dla przeciwnych argumentów wartości cosinusa są takie same. Dlatego zmiana kolejności wektorów przy mnożeniu skalarnym nie ma wpływu na wartość wyniku.
Wzór nr 3: Wartość iloczynu skalarnego wektorów jest równa iloczynowi długości razy cosinus kąta zawartego między tymi wektorami. Jeśli wartość tego iloczynu jest równa 0 oznacza to, że jeden (lub obydwa jednocześnie) z wektorów jest wektorem zerowym lub cosinus kąta jest równy 0 (wektory są prostopadłe).
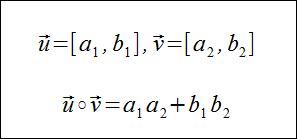
Sprawdź czy wektory u[1,3] i v[-6,2] są prostopadłe.
Rozwiązanie
Obydwa podane wektory są niezerowe. Oznacza to, że jeśli ich iloczyn skalarny będzie równy 0 to będą one prostopadłe. Do obliczenia iloczynu skalarnego zastosujemy podane twierdzenie:
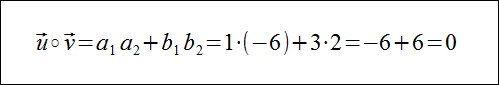
Iloczyn skalarny wektorów jest równy 0 co oznacza, że dane dwa wektory są prostopadłe.
Przykład 2
Dane są dwa wektory a i b o długościach 4 i 5. Kąt (a,b) między tymi wektorami ma miarę 60 stopni. Oblicz iloczyn skalarny wektorów a i b.
Rozwiązanie
Podstawiamy dane do wzoru: a º b = 4 * 5 * cos(60) = 4 * 5 * 0.5 = 10
Iloczyn skalarny wektorów - definicja
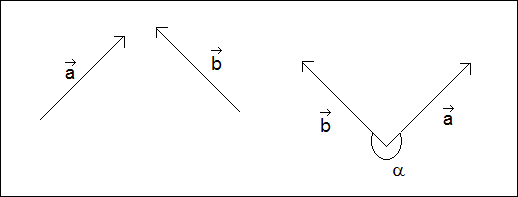
Niech będą dane dwa wektory a i b. Kątem pary wektorów (a,b) nazywamy kąt, którego jedno ramię ma kierunek i zwrot wektora a, drugie zaś ma kierunek i zwrot wektora b. Obrazuje to następujący rysunek:
Iloczyn skalarny dwóch niezerowych wektorów jest równy iloczynowi długości wektorów razy cosinus kąta zawartego między nimi. Wyrażamy to następującym wzorem:
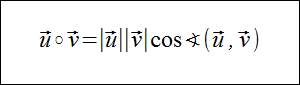
Iloczyn skalarny wektorów- własności
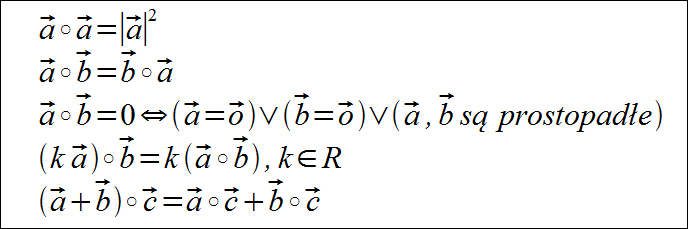
Wyjaśnienia kilku z powyższych wzorów:
Wzór nr 1: Jeśli mamy dwa identyczne wektory to kąt między nimi jest równy 0 °. cos 0 ° = 1 zatem iloczyn skalarny tych wektorów będzie równy iloczynowi ich (identycznych) długości razy 1 czyli będzie równy kwadratowi długości.
Wzór nr 2: Jeśli zmienimy kolejność wektorów przy mnożeniu skalarnym, ich długości się nie zmienią. Zmieni się jedynie kąt między nimi na przeciwny. Jednak jak wiadomo funkcja cosinus jest funkcją parzystą - dla przeciwnych argumentów wartości cosinusa są takie same. Dlatego zmiana kolejności wektorów przy mnożeniu skalarnym nie ma wpływu na wartość wyniku.
Wzór nr 3: Wartość iloczynu skalarnego wektorów jest równa iloczynowi długości razy cosinus kąta zawartego między tymi wektorami. Jeśli wartość tego iloczynu jest równa 0 oznacza to, że jeden (lub obydwa jednocześnie) z wektorów jest wektorem zerowym lub cosinus kąta jest równy 0 (wektory są prostopadłe).
Iloczyn skalarny wektorów - twierdzenie
Poniższe twierdzenie umożliwia obliczenie wartości iloczynu skalarnego dwóch wektorów w przypadku gdy znamy tylko ich współrzędne. Niech dane będą dwa wektory u=[a1,b1] i v=[a2,b2]. Wówczas iloczyn skalarny tych wektorów jest równy: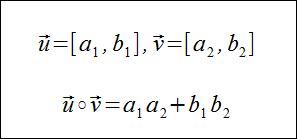
Iloczyn skalarny wektorów - przykłady
Przykład 1Sprawdź czy wektory u[1,3] i v[-6,2] są prostopadłe.
Rozwiązanie
Obydwa podane wektory są niezerowe. Oznacza to, że jeśli ich iloczyn skalarny będzie równy 0 to będą one prostopadłe. Do obliczenia iloczynu skalarnego zastosujemy podane twierdzenie:
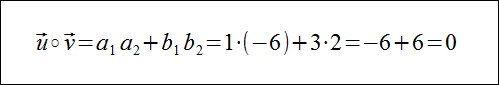
Iloczyn skalarny wektorów jest równy 0 co oznacza, że dane dwa wektory są prostopadłe.
Przykład 2
Dane są dwa wektory a i b o długościach 4 i 5. Kąt (a,b) między tymi wektorami ma miarę 60 stopni. Oblicz iloczyn skalarny wektorów a i b.
Rozwiązanie
Podstawiamy dane do wzoru: a º b = 4 * 5 * cos(60) = 4 * 5 * 0.5 = 10