Strona główna > Matematyka > Funkcje > Funkcja homograficzna
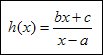
gdzie b i c nie są równocześnie równe 0.
Najprostszym przypadkiem funkcji homograficznej jest jest funkcja:
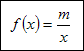
Jej wykresem jest krzywa zwana hiperbolą. Dla m > 0 wygląda ona następująco:
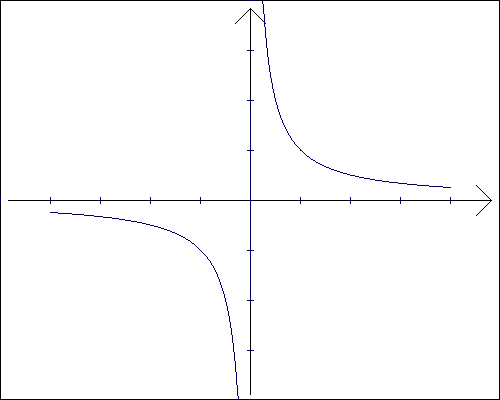
Gdy hiperbolę przesuniemy o wektor u=[a,b] to otrzymamy funkcję:
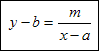
Po przekształceniach otrzymujemy:
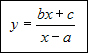
Przykład 1
Należy narysować wykres funkcji danej wzorem:
Zatem dana funkcja jest równoważna:
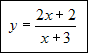
Dzielimy licznik przez mianownik:
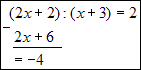
Zatem dana funkcja jest równoważna następującej funkcji:
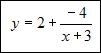
Czyli otrzymujemy:
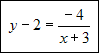
Z podanego wzoru odczytujemy współrzędne wektora przesunięcia u[-3 , 2]
Oznacza to, że aby narysować wykres danej funkcji należy wykres funkcji y=-4/x przesunąć o wektor u[-3 , 2]. Oto szukany wykres (na wykresie zaznaczono wektor przesunięcia u):

2013-04-28 15:30:36 asdfghjkl napisał(a):
zadanie 4, podpunkty e,f oraz g. proszę o pomoc

2013-04-28 21:45:15 BazyWiedzy.COM napisał(a):
e) (x-1)/(x-4) > 0 wtedy i tylko wtedy, gdy (x-1)*(x-4) > 0
Aby f(x) przyjmowała wartości dodanie : x należy do przedziału (-nieskończoność , 1) u (4, nieskończoność)
(x-1)/(x-4) < 0 wtedy i tylko wtedy, gdy (x-1)*(x-4) < 0
Aby f(x) przyjmowała wartości ujemne : x należy do przedziału (1,4).
f) f(0) = (0-1)/(0-4) = -1/-4=1/4
g) f(7) = (7-1)/(7-4) = 6/3=2
Funkcja homograficzna
Funkcja homograficzna to funkcja dana wzorem: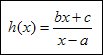
gdzie b i c nie są równocześnie równe 0.
Najprostszym przypadkiem funkcji homograficznej jest jest funkcja:
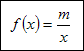
Jej wykresem jest krzywa zwana hiperbolą. Dla m > 0 wygląda ona następująco:

Gdy hiperbolę przesuniemy o wektor u=[a,b] to otrzymamy funkcję:
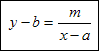
Po przekształceniach otrzymujemy:
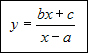
Przykład 1
Należy narysować wykres funkcji danej wzorem:
Zatem dana funkcja jest równoważna:
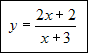
Dzielimy licznik przez mianownik:
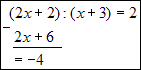
Zatem dana funkcja jest równoważna następującej funkcji:
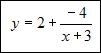
Czyli otrzymujemy:
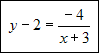
Z podanego wzoru odczytujemy współrzędne wektora przesunięcia u[-3 , 2]
Oznacza to, że aby narysować wykres danej funkcji należy wykres funkcji y=-4/x przesunąć o wektor u[-3 , 2]. Oto szukany wykres (na wykresie zaznaczono wektor przesunięcia u):

Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (2)
2013-04-28 15:30:36 asdfghjkl napisał(a):
zadanie 4, podpunkty e,f oraz g. proszę o pomoc

2013-04-28 21:45:15 BazyWiedzy.COM napisał(a):
e) (x-1)/(x-4) > 0 wtedy i tylko wtedy, gdy (x-1)*(x-4) > 0
Aby f(x) przyjmowała wartości dodanie : x należy do przedziału (-nieskończoność , 1) u (4, nieskończoność)
(x-1)/(x-4) < 0 wtedy i tylko wtedy, gdy (x-1)*(x-4) < 0
Aby f(x) przyjmowała wartości ujemne : x należy do przedziału (1,4).
f) f(0) = (0-1)/(0-4) = -1/-4=1/4
g) f(7) = (7-1)/(7-4) = 6/3=2