Strona główna > Matematyka > Wyrażenia algebraiczne > Działania na potęgach
an · am = an+m
Aby łatwo zapamiętać ten wzór wystarczy zapisać sobie następujące (lub podobne) przykładowe działanie:
22 · 23 = (2 · 2) · (2 · 2 · 2 ) = 2 · 2 · 2 · 2 · 2 = 25 = 2 2+3
Dzielenie potęg o jednakowych podstawach.
an : am = an-m
W zapamiętaniu tego wzoru może pomóc następujący przykład (lub podobny):
23 / 22 = 2 · 2 · 2 / 2 ·2 = 2 = 21 = 23-2
Potęga potęgi.
( an ) m = an · m
W zapamiętaniu tego wzoru może pomóc następujące działanie:
(22)3 = 22 · 22 · 22 = 2 · 2 · 2 · 2 · 2 · 2 = 26 = 22 · 3
Mnożenie potęg o jednakowych wykładnikach.
an · bn = (a · b)n
Dzielenie potęg o jednakowych wykładnikach.
an : bn = (a : b)n dla b różnego od 0
Przykład 1
Należy obliczyć wartość wyrażenia:
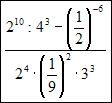
Rozwiązanie

2012-09-25 00:23:40 Matma napisał(a):
Artykuł był przydatny , dzięki niemu lepiej rozumiem te całe potęgi ;-)
2012-09-26 16:58:19 Moka napisał(a):
Poproszę o łatwiejszy wzór :)
2012-10-22 15:48:26 Moka napisał(a):
Poproszę o łatwiejszy wzór :)
2012-11-27 15:18:44 Kelman napisał(a):
Wielkie dzięki! Już łatwiej chyba się nie da wytłumaczyć...
2012-12-25 13:57:53 volpad napisał(a):
lepiej nie da się wytłumaczyć
2013-01-06 23:23:33 Gość napisał(a):
Wszystko skumałem tzn. niby kumam ale jak patrze na rozwiązanie to nic nie kumam ;/
2013-03-15 14:25:28 gniewko napisał(a):
Do kompletu brakuje tylko przykładu w jaki sposób należy liczyć potęgi minusowe oraz ułamki z potęgą minusową. Natomiast rozwiązanie przykładu zaciemnia sposób rozwiązania.
2013-05-27 23:00:20 Gościu napisał(a):
dzięki, bardzo mi to pomogło, naprawdę, niby tylko jeden przykład, a tu niespodzianka :D
2015-09-14 16:54:36 napisał(a):
Mam pytanie w 4 słupku w liczniku jest 2^4 -2^5 a w następnej części już jest 2^4 (1-2^2) skąd sie wzieło to (1-2^2) ??
2015-09-14 19:14:33 Just me napisał(a):
Bardzo przydatne i łatwe wytłumaczenie Dobrze, że są podane przykłady :)
2015-09-14 19:41:26 BazyWiedzy.COM napisał(a):
Witaj. W czwartym słupku w liczniku jest 2^4-2^6 a nie tak jak napisałeś/aś 2^4-2^5. Oto skąd się to wzięło: 2^4-2^6 = 1 * 2^4 - 2^2 * 2^4 Przy rozbijaniu 2^6 na 2^2 * 2^4 korzystamy ze wzoru na mnożenie potęg o jednakowych podstawach. Dalej z otrzymanej różnicy 1 * 2^4 - 2^2 * 2^4 możemy wyłączyć wspólny czynnik 2^4 przed nawias: 1 * 2^4 - 2^2 * 2^4 = 2^4 * (1 - 2^2). Czy teraz jest już wszystko jasne :-) ? Pozdrawiam BazyWiedzy.COM
2015-09-14 19:45:14 BazyWiedzy.COM napisał(a):
do Just me : dziękuję za miłe słowa :-) Pozdrawiam.
Działania na potęgach
Mnożenie potęg o jednakowych podstawach.an · am = an+m
Aby łatwo zapamiętać ten wzór wystarczy zapisać sobie następujące (lub podobne) przykładowe działanie:
22 · 23 = (2 · 2) · (2 · 2 · 2 ) = 2 · 2 · 2 · 2 · 2 = 25 = 2 2+3
Dzielenie potęg o jednakowych podstawach.
an : am = an-m
W zapamiętaniu tego wzoru może pomóc następujący przykład (lub podobny):
23 / 22 = 2 · 2 · 2 / 2 ·2 = 2 = 21 = 23-2
Potęga potęgi.
( an ) m = an · m
W zapamiętaniu tego wzoru może pomóc następujące działanie:
(22)3 = 22 · 22 · 22 = 2 · 2 · 2 · 2 · 2 · 2 = 26 = 22 · 3
Mnożenie potęg o jednakowych wykładnikach.
an · bn = (a · b)n
Dzielenie potęg o jednakowych wykładnikach.
an : bn = (a : b)n dla b różnego od 0
Przykład 1
Należy obliczyć wartość wyrażenia:
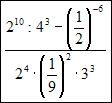
Rozwiązanie

Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (12)
2012-09-25 00:23:40 Matma napisał(a):
Artykuł był przydatny , dzięki niemu lepiej rozumiem te całe potęgi ;-)
2012-09-26 16:58:19 Moka napisał(a):
Poproszę o łatwiejszy wzór :)
2012-10-22 15:48:26 Moka napisał(a):
Poproszę o łatwiejszy wzór :)
2012-11-27 15:18:44 Kelman napisał(a):
Wielkie dzięki! Już łatwiej chyba się nie da wytłumaczyć...
2012-12-25 13:57:53 volpad napisał(a):
lepiej nie da się wytłumaczyć
2013-01-06 23:23:33 Gość napisał(a):
Wszystko skumałem tzn. niby kumam ale jak patrze na rozwiązanie to nic nie kumam ;/
2013-03-15 14:25:28 gniewko napisał(a):
Do kompletu brakuje tylko przykładu w jaki sposób należy liczyć potęgi minusowe oraz ułamki z potęgą minusową. Natomiast rozwiązanie przykładu zaciemnia sposób rozwiązania.
2013-05-27 23:00:20 Gościu napisał(a):
dzięki, bardzo mi to pomogło, naprawdę, niby tylko jeden przykład, a tu niespodzianka :D
2015-09-14 16:54:36 napisał(a):
Mam pytanie w 4 słupku w liczniku jest 2^4 -2^5 a w następnej części już jest 2^4 (1-2^2) skąd sie wzieło to (1-2^2) ??
2015-09-14 19:14:33 Just me napisał(a):
Bardzo przydatne i łatwe wytłumaczenie Dobrze, że są podane przykłady :)
2015-09-14 19:41:26 BazyWiedzy.COM napisał(a):
Witaj. W czwartym słupku w liczniku jest 2^4-2^6 a nie tak jak napisałeś/aś 2^4-2^5. Oto skąd się to wzięło: 2^4-2^6 = 1 * 2^4 - 2^2 * 2^4 Przy rozbijaniu 2^6 na 2^2 * 2^4 korzystamy ze wzoru na mnożenie potęg o jednakowych podstawach. Dalej z otrzymanej różnicy 1 * 2^4 - 2^2 * 2^4 możemy wyłączyć wspólny czynnik 2^4 przed nawias: 1 * 2^4 - 2^2 * 2^4 = 2^4 * (1 - 2^2). Czy teraz jest już wszystko jasne :-) ? Pozdrawiam BazyWiedzy.COM
2015-09-14 19:45:14 BazyWiedzy.COM napisał(a):
do Just me : dziękuję za miłe słowa :-) Pozdrawiam.