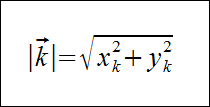Strona główna > Matematyka > Wektory > Długość wektora

Rozwiązanie
Podstawiamy współrzędne wektora do wzoru na długość:
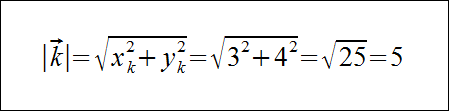
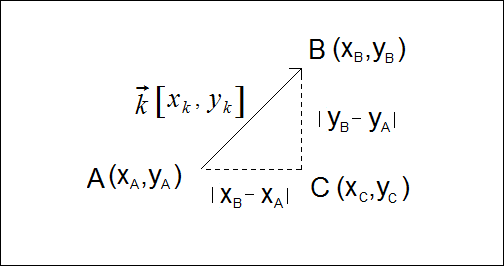
Długość przeciwprostokątnej tego trójkąta będzie szukaną długością wektora k. Z twierdzenia Pitagorasa obliczmy długość przeciwprostokątnej:
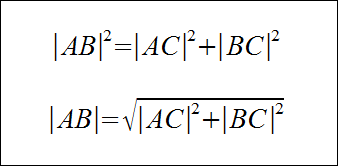
Długości przyprostokątnych trójkąta ABC są równe:
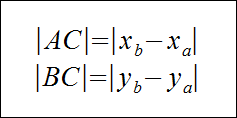
Stąd otrzymujemy:
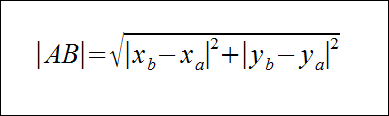
Ponieważ |a|2 = a2 to w powyższym wzorze możemy opuścić wartości bezwzględne.

Wiadomo, że współrzędne wektora dane są równaniami :
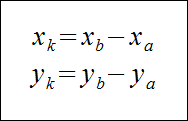
Stąd otrzymujemy wzór na długość wektora:
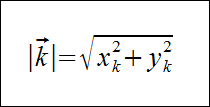
Długość wektora
Dla danego wektora k o współrzędnych xk, yk jego długość jest równa pierwiastkowi kwadratowemu z sumy kwadratów jego współrzędnych:
Długość wektora - przykład
Dany jest wektor k o współrzędnych xk=3, yk=4. Oblicz jego długość.Rozwiązanie
Podstawiamy współrzędne wektora do wzoru na długość:
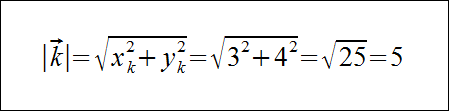
Wyprowadzenie wzoru na długość wektora
Niech dany będzie wektor k o początku w punkcie A (xa , ya) i końcu w punkcie B (xb, yb). Rozpatrzmy trójkąt prostokątny ABC (patrz rysunek):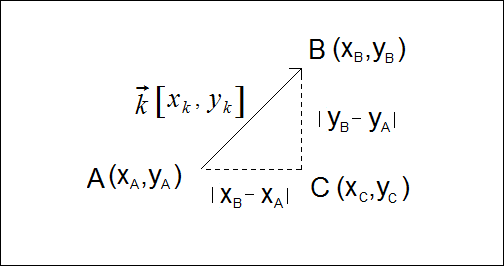
Długość przeciwprostokątnej tego trójkąta będzie szukaną długością wektora k. Z twierdzenia Pitagorasa obliczmy długość przeciwprostokątnej:
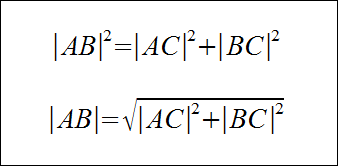
Długości przyprostokątnych trójkąta ABC są równe:
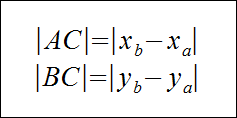
Stąd otrzymujemy:
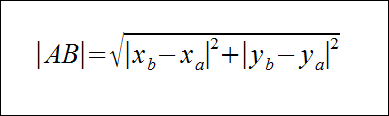
Ponieważ |a|2 = a2 to w powyższym wzorze możemy opuścić wartości bezwzględne.

Wiadomo, że współrzędne wektora dane są równaniami :
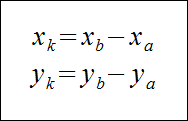
Stąd otrzymujemy wzór na długość wektora: