Strona główna > Matematyka > Ciągi liczbowe > Ciąg arytmetyczny
Dla każdego n należącego do zbioru liczb naturalnych dodatnich wartość an+1-an jest stała i równa r. Liczba r jest nazywana różnicą ciągu arytmetycznego.
a2-a1=r , stąd: a2=a1+r
a3-a2=r , stąd : a3=a2+r= a1+r+r=a1+2r
a3=a1+2r
a4-a3=r
a4=a3+r
a4=a1+2r+r=a1+3r
a4=a1+3r
Łatwo wydedukować jaki będzie wzór na n-ty wyraz ciągu arytmetycznego:
an=a1+(n-1)r
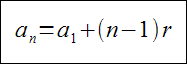
Uzasadnienie:
20-17=3
17-14=3
14-11=3
11-8=3
8-5=3
5-2=3
Powyższy ciąg jest ciągiem arytmetycznym o różnicy r=3.
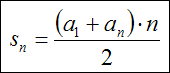
Gdzie : a1 - pierwszy element ciągu , an - n-ty element ciągu
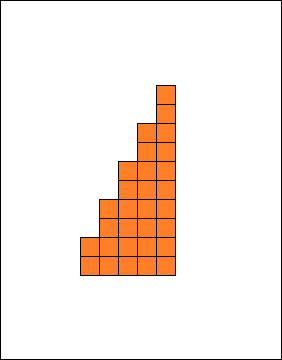
Na podstawie otrzymanej figury zbudujmy prostokąt. Pole prostokąta będzie równe dwukrotności pola rozpatrywanej figury. Naszym celem jest wyznaczyć pole figury, które liczbowo będzie równe sumie ciągu arytmetycznego. Pole prostokąta jest równe iloczynowi długości boków. Patrząc na rysunek łatwo zauważyć, że będzie ono równe (a1+an)n. Stąd szukane pole figury będzie równe połowie pola prostokąta: P=(a1+an)n/2. Jest to jednocześnie suma wszystkich elementów ciągu arytmetycznego.
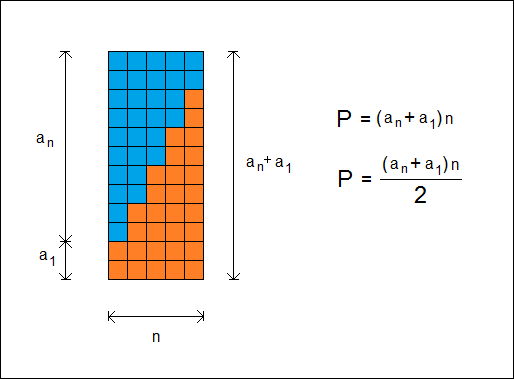
Dany jest ciąg o wyrazie ogólnym bn=4n+12. Udowodnij, że ten ciąg jest ciągiem arytmetycznym.
Zadanie 1 - rozwiązanie
Aby udowodnić, że ciąg jest ciągiem arytmetycznym wystarczy dowieść, że różnica kolejnych elementów ciągu jest stała.
n-ty element : bn = 4n+12
n+1 element : bn+1 = 4(n+1)+12=4n+16
Różnica kolejnych elementów: bn+1 - bn = 4n+16-(4n+12)=4n+16-4n-12=4
c.n.d.
Zadanie 2
Udowodnij, że dany ciąg arytmetyczny o wyrazie ogólnym an=3n-1 jest rosnący.
Zadanie 2 - rozwiązanie
an = 3n-1
an+1 = 3(n+1)-1=3n+3-1=3n+2
Aby zbadać monotoniczność ciągu badamy różnicę: an+1 - an = 3n+2 - (3n-1)=3n+2-3n+1=3
Ze względu na to, że różnica r>0 możemy stwierdzić, że ciąg jest rosnący.
2012-09-27 22:06:25 Krzychu napisał(a):
b.dobre wytłumaczenie. Dzięki ;) PS napiszcie gdzieś jak można wspomóc stronkę :]
2012-09-28 22:58:31 BazyWiedzy.COM napisał(a):
Dziękujemy za komentarz. Jeśli na naszej stronie znalazłeś przydatne informacje, rozwiązanie zadania, wyjaśnienie jakiegoś problemu i chciałbyś nam pomóc będziemy bardzo wdzięczni. Oto jak możesz to zrobić.
1. Powiedz komuś o nas. Możesz wysłać maila do przyjaciela z linkiem lub informacją o naszej stronie lub kliknąć "lubię to", +1 (przycisk znajduje się na górze artykułów).
2. Jeśli udzielasz się na forach w Internecie możesz w trakcie jakiejś dyskusji podać link do naszej strony lub do artykułu.
3. Jeśli masz jakiś pomysł jak ulepszyć naszą stronę napisz do nas.
4. Jeśli interesują Cię doświadczenia chemiczne możesz zasubskrybować nasz kanał na Youtube http://www.youtube.com/user/BazyWiedzyCOM.
5. Jeśli posiadasz stronę www lub blog i możesz umieścić link do naszej strony.
2012-12-10 18:37:30 ToMEk napisał(a):
Fajna stronka
2013-03-20 19:54:50 ania napisał(a):
Moje zadanka:D Są to zadania zamknięte.
1.Dany jest ciąg an=n^2-4.Wówczas an=0 gdy:
a).N=0
b).n=2 lub n=-2
c).tylko n=2
d).n=-4
2.Dany jest ciąg arytmetyczny o wyrazie ogólnym an=5n+3.Różnica tego ciągu jest
równa:
a).R=3
b).r=-3
c).r=5
d).r=-5
3.Liczby 4x+5,x,7 tworzą w podanej kolejności ciąg arytmetyczny.Wskaż liczbę x.
a).x=7/4
b).x=-7/4
c).x=4/7
d).x=-4/7
Teraz będą trzy zadania otwarte.
1.W ciągu arytmetycznym a1=4,S3=27.Wyznacz różnicę tego ciągu.
2.Dany jest ciąg arytmetyczny (x^2,2x,). Wyznacz liczbę x.
3.Dany jest ciąg o wyrazie ogólnym an=(2n+4)(n+7)(n-9). Sprawdź, który wyraz ciągu jest równy 0.
2013-03-20 20:28:36 BazyWiedzy.COM napisał(a):
Witaj.
Zadania otwarte:
Zadanie 1.
Za n można wstawić tylko liczbę naturalną. Dla ciągu o an=n2-4. W tym przypadku an=0 gdy n=2. Odpowiedź c)
Zadanie 2.
Różnica r=an+1-an=5(n+1)+3-(5n+3) =5n+5+3-5n-3=5. Właściwa odpowiedź c).
Zadanie 3.
Jeśli te liczby tworzą ciąg arytmetyczny to prawdziwa jest równość:
7-x=x-(4x+5)
7-x=x-4x-5
-x-x+4x=-5-7
2x=-12 |:2
x=-6
Coś się nie zgadza bo nie ma takiej odpowiedzi - sprawdź czy dobrze przepisałaś to zadanie.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-20 20:39:59 BazyWiedzy.COM napisał(a):
Witaj.
Zadania zamknięte:
Zadanie 1.
S3=(a1+a3)*3/2
27=(4+a3)*3/2 |*2/3
18=(4+a3)
18-4=a3
14=a3
Czyli mamy : a1=4 i a3=14. Wiadomo, że a3 = a1 +2r. Czyli mamy:
14=4+2*r
14-4=2*r
10=2 * r
r=5
W zadaniu 2 chyba brakuje jednej liczby.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-20 21:50:11 anna napisał(a):
Witam, W obu tych zadaniach jest tak jak napisałam:(
2013-03-20 21:55:54 BazyWiedzy.COM napisał(a):
Ok. Jeszcze pomyślę nad tymi dwoma zadaniami. Tymczasem zrobię 3:
an=(2n+4)(n+7)(n-9)
Wiadomo, że n jest liczbą naturalną. Przy takim założeniu podany iloczyn zeruje się tylko dla liczby 9.
2013-03-20 22:00:57 anna napisał(a):
Witam, Mój błąd bo się pogubiłam w zad.2 jest jeszcze liczba 3
2013-03-20 22:38:08 BazyWiedzy.COM napisał(a):
Ok. To teraz można zrobić to zadanie :-)
Jeśli dane liczby x2,2x,3 są ciągiem arytmetycznym to musi być spełnione równanie:
3-2x=2x-x2
3-2x-2x+x2 = 0
x2 - 4x +3 = 0
Δ = 16-4*1*3= 16-12=4
√ Δ = 2
x1= (-b-√ Δ)/(2a)=(4-2)/2=1
x2= (-b+√ Δ)/(2a)=(4+2)/2=3
Odp.: x=1 lub x=3
Pozdrawiam
Marcin - BazyWiedzy.COM
Ciąg arytmetyczny
Ciąg arytmetyczny an to ciąg liczbowy, w którym spełniony jest warunek:Dla każdego n należącego do zbioru liczb naturalnych dodatnich wartość an+1-an jest stała i równa r. Liczba r jest nazywana różnicą ciągu arytmetycznego.
Wzór na n-ty element ciągu arytmetycznego
Wyznaczmy elementy a2, a3 i a4 w zależności od a1 i r:a2-a1=r , stąd: a2=a1+r
a3-a2=r , stąd : a3=a2+r= a1+r+r=a1+2r
a3=a1+2r
a4-a3=r
a4=a3+r
a4=a1+2r+r=a1+3r
a4=a1+3r
Łatwo wydedukować jaki będzie wzór na n-ty wyraz ciągu arytmetycznego:
an=a1+(n-1)r
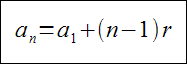
Przykład ciągu arytmetycznego.
2, 5, 8, 11, 14, 17, 20 ...Uzasadnienie:
20-17=3
17-14=3
14-11=3
11-8=3
8-5=3
5-2=3
Powyższy ciąg jest ciągiem arytmetycznym o różnicy r=3.
Suma n pierwszych elementów ciągu arytmetycznego.
Oto wzór na sumę n pierwszych elementów ciągu arytmetycznego: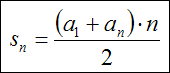
Gdzie : a1 - pierwszy element ciągu , an - n-ty element ciągu
Suma ciągu arytmetycznego - wyjaśnienie wzoru
Przedstawmy ciąg arytmetyczny w postaci graficznej: jeden kwadracik obrazuje wartość liczbową równą 1. Każdy element ciągu to pionowy zestaw kwadracików. Pierwszy element tego ciągu będzie miał wartość a1=2 a różnica ciągu r=2. Nasz ciąg będzie się składał z pięciu elementów czyli n=5. Sumą wszystkich elementów ciągu będzie łączna ilość wszystkich kwadracików.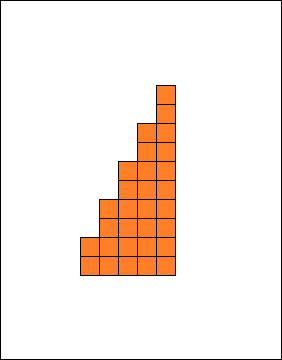
Na podstawie otrzymanej figury zbudujmy prostokąt. Pole prostokąta będzie równe dwukrotności pola rozpatrywanej figury. Naszym celem jest wyznaczyć pole figury, które liczbowo będzie równe sumie ciągu arytmetycznego. Pole prostokąta jest równe iloczynowi długości boków. Patrząc na rysunek łatwo zauważyć, że będzie ono równe (a1+an)n. Stąd szukane pole figury będzie równe połowie pola prostokąta: P=(a1+an)n/2. Jest to jednocześnie suma wszystkich elementów ciągu arytmetycznego.
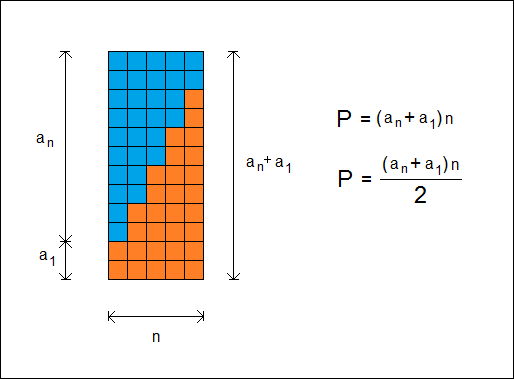
Ciąg arytmetyczny - przykładowe zadania.
Zadanie 1Dany jest ciąg o wyrazie ogólnym bn=4n+12. Udowodnij, że ten ciąg jest ciągiem arytmetycznym.
Zadanie 1 - rozwiązanie
Aby udowodnić, że ciąg jest ciągiem arytmetycznym wystarczy dowieść, że różnica kolejnych elementów ciągu jest stała.
n-ty element : bn = 4n+12
n+1 element : bn+1 = 4(n+1)+12=4n+16
Różnica kolejnych elementów: bn+1 - bn = 4n+16-(4n+12)=4n+16-4n-12=4
c.n.d.
Zadanie 2
Udowodnij, że dany ciąg arytmetyczny o wyrazie ogólnym an=3n-1 jest rosnący.
Zadanie 2 - rozwiązanie
an = 3n-1
an+1 = 3(n+1)-1=3n+3-1=3n+2
Aby zbadać monotoniczność ciągu badamy różnicę: an+1 - an = 3n+2 - (3n-1)=3n+2-3n+1=3
Ze względu na to, że różnica r>0 możemy stwierdzić, że ciąg jest rosnący.
Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (10)
2012-09-27 22:06:25 Krzychu napisał(a):
b.dobre wytłumaczenie. Dzięki ;) PS napiszcie gdzieś jak można wspomóc stronkę :]
2012-09-28 22:58:31 BazyWiedzy.COM napisał(a):
Dziękujemy za komentarz. Jeśli na naszej stronie znalazłeś przydatne informacje, rozwiązanie zadania, wyjaśnienie jakiegoś problemu i chciałbyś nam pomóc będziemy bardzo wdzięczni. Oto jak możesz to zrobić.
1. Powiedz komuś o nas. Możesz wysłać maila do przyjaciela z linkiem lub informacją o naszej stronie lub kliknąć "lubię to", +1 (przycisk znajduje się na górze artykułów).
2. Jeśli udzielasz się na forach w Internecie możesz w trakcie jakiejś dyskusji podać link do naszej strony lub do artykułu.
3. Jeśli masz jakiś pomysł jak ulepszyć naszą stronę napisz do nas.
4. Jeśli interesują Cię doświadczenia chemiczne możesz zasubskrybować nasz kanał na Youtube http://www.youtube.com/user/BazyWiedzyCOM.
5. Jeśli posiadasz stronę www lub blog i możesz umieścić link do naszej strony.
2012-12-10 18:37:30 ToMEk napisał(a):
Fajna stronka
2013-03-20 19:54:50 ania napisał(a):
Moje zadanka:D Są to zadania zamknięte.
1.Dany jest ciąg an=n^2-4.Wówczas an=0 gdy:
a).N=0
b).n=2 lub n=-2
c).tylko n=2
d).n=-4
2.Dany jest ciąg arytmetyczny o wyrazie ogólnym an=5n+3.Różnica tego ciągu jest
równa:
a).R=3
b).r=-3
c).r=5
d).r=-5
3.Liczby 4x+5,x,7 tworzą w podanej kolejności ciąg arytmetyczny.Wskaż liczbę x.
a).x=7/4
b).x=-7/4
c).x=4/7
d).x=-4/7
Teraz będą trzy zadania otwarte.
1.W ciągu arytmetycznym a1=4,S3=27.Wyznacz różnicę tego ciągu.
2.Dany jest ciąg arytmetyczny (x^2,2x,). Wyznacz liczbę x.
3.Dany jest ciąg o wyrazie ogólnym an=(2n+4)(n+7)(n-9). Sprawdź, który wyraz ciągu jest równy 0.
2013-03-20 20:28:36 BazyWiedzy.COM napisał(a):
Witaj.
Zadania otwarte:
Zadanie 1.
Za n można wstawić tylko liczbę naturalną. Dla ciągu o an=n2-4. W tym przypadku an=0 gdy n=2. Odpowiedź c)
Zadanie 2.
Różnica r=an+1-an=5(n+1)+3-(5n+3) =5n+5+3-5n-3=5. Właściwa odpowiedź c).
Zadanie 3.
Jeśli te liczby tworzą ciąg arytmetyczny to prawdziwa jest równość:
7-x=x-(4x+5)
7-x=x-4x-5
-x-x+4x=-5-7
2x=-12 |:2
x=-6
Coś się nie zgadza bo nie ma takiej odpowiedzi - sprawdź czy dobrze przepisałaś to zadanie.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-20 20:39:59 BazyWiedzy.COM napisał(a):
Witaj.
Zadania zamknięte:
Zadanie 1.
S3=(a1+a3)*3/2
27=(4+a3)*3/2 |*2/3
18=(4+a3)
18-4=a3
14=a3
Czyli mamy : a1=4 i a3=14. Wiadomo, że a3 = a1 +2r. Czyli mamy:
14=4+2*r
14-4=2*r
10=2 * r
r=5
W zadaniu 2 chyba brakuje jednej liczby.
Pozdrawiam
Marcin - BazyWiedzy.COM
2013-03-20 21:50:11 anna napisał(a):
Witam, W obu tych zadaniach jest tak jak napisałam:(
2013-03-20 21:55:54 BazyWiedzy.COM napisał(a):
Ok. Jeszcze pomyślę nad tymi dwoma zadaniami. Tymczasem zrobię 3:
an=(2n+4)(n+7)(n-9)
Wiadomo, że n jest liczbą naturalną. Przy takim założeniu podany iloczyn zeruje się tylko dla liczby 9.
2013-03-20 22:00:57 anna napisał(a):
Witam, Mój błąd bo się pogubiłam w zad.2 jest jeszcze liczba 3
2013-03-20 22:38:08 BazyWiedzy.COM napisał(a):
Ok. To teraz można zrobić to zadanie :-)
Jeśli dane liczby x2,2x,3 są ciągiem arytmetycznym to musi być spełnione równanie:
3-2x=2x-x2
3-2x-2x+x2 = 0
x2 - 4x +3 = 0
Δ = 16-4*1*3= 16-12=4
√ Δ = 2
x1= (-b-√ Δ)/(2a)=(4-2)/2=1
x2= (-b+√ Δ)/(2a)=(4+2)/2=3
Odp.: x=1 lub x=3
Pozdrawiam
Marcin - BazyWiedzy.COM