Strona główna > Matematyka > Funkcje > Asymptoty funkcji
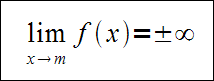
Jeśli odpowiednia granica istnieje, wówczas asymptota pionowa będzie miała równanie:

Jako punkty, przez które może przechodzić asymptota pionowa wybieramy punkty na krańcach przedziału określoności, te w których wartość funkcji nie istnieje.
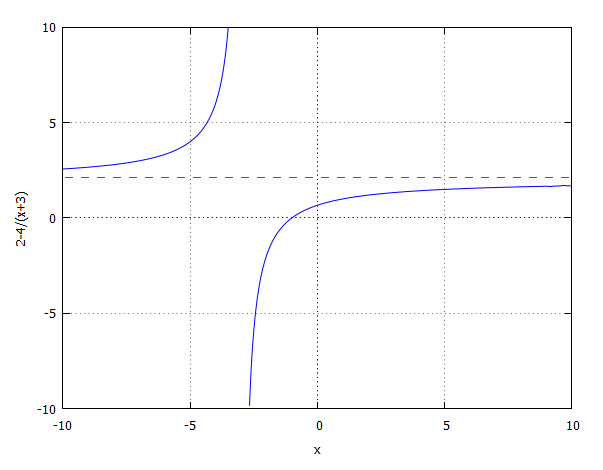
Funkcja ta jest określona w przedziale ( - ∞ , -3 ) lub (-3 , ∞). W punkcie x=-3 funkcja nie istnieje. Sprawdzamy zatem granicę lewostronną i prawostronną w tym punkcie:
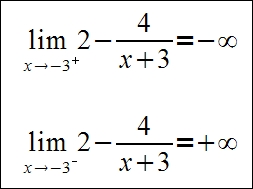
Asymptota pionowa ma więc wzór: x=-3. Poniżej pokazujemy wykres analizowanej funkcji z zaznaczoną na czerwono asymptotą pionową. Zgodnie z obliczonymi granicami gdy "zbliżamy się" do punktu x=-3 z lewej strony to funkcja zmierza do ∞. Gdy "zbliżamy się" do punktu x=-3 z prawej strony to funkcja zmierza do -∞.

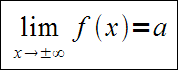
Jeśli odpowiednia granica istnieje, wówczas asymptota pozioma będzie miała wzór:

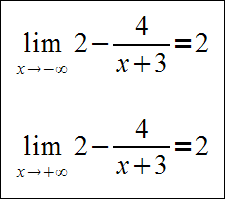
Asymptota pozioma funkcji homograficznej ma wzór y=2.
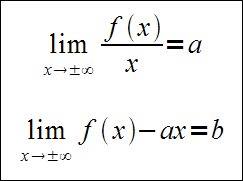
to asymptota ukośna funkcji f(x) ma wzór:

Wyznaczamy granicę (współczynnik a):

Wyznaczamy granicę (współczynnik b):
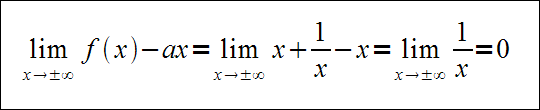
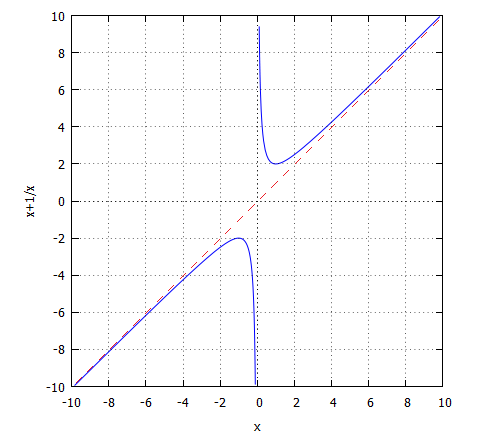
Równanie asymptoty ukośnej będzie miało postać: y=x.
2012-11-29 15:43:46 napisał(a):
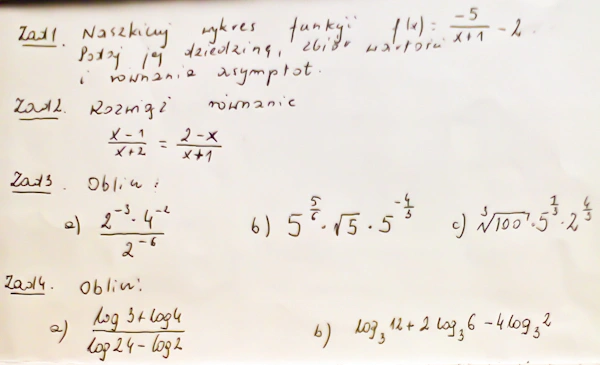
2012-11-29 23:32:11 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie zadania nr 2:
W pierwszej kolejności zakładamy, że x jest różne od -2 oraz od -1 (dlatego, że liczby te zerują mianowniki ułamków).
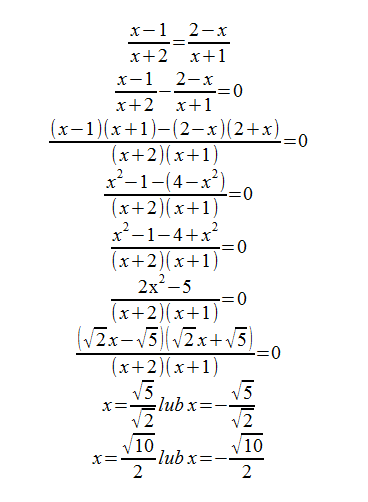
2012-12-01 18:11:13 BazyWiedzy.COM napisał(a):
Oto rozwiązanie zadania 3.

Asymptoty funkcji - asymptota pionowa
Z asymptotą pionową mamy do czynienia wtedy, gdy istnieje granica funkcji: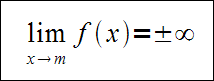
Jeśli odpowiednia granica istnieje, wówczas asymptota pionowa będzie miała równanie:

Jako punkty, przez które może przechodzić asymptota pionowa wybieramy punkty na krańcach przedziału określoności, te w których wartość funkcji nie istnieje.
Asymptota pionowa - przykład
Należy wyznaczyć asymptotę pionową funkcji homograficznej y=2-4/(x+3)Funkcja ta jest określona w przedziale ( - ∞ , -3 ) lub (-3 , ∞). W punkcie x=-3 funkcja nie istnieje. Sprawdzamy zatem granicę lewostronną i prawostronną w tym punkcie:
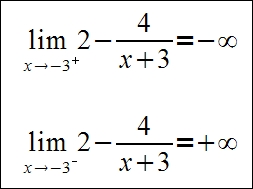
Asymptota pionowa ma więc wzór: x=-3. Poniżej pokazujemy wykres analizowanej funkcji z zaznaczoną na czerwono asymptotą pionową. Zgodnie z obliczonymi granicami gdy "zbliżamy się" do punktu x=-3 z lewej strony to funkcja zmierza do ∞. Gdy "zbliżamy się" do punktu x=-3 z prawej strony to funkcja zmierza do -∞.

Asymptoty funkcji - asymptota pozioma
Asymptoty poziome mogą istnieć jeśli dziedzina funkcji rozciąga się do nieskończoności. Jeśli istnieje odpowiednia granica funkcji: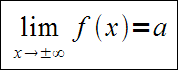
Jeśli odpowiednia granica istnieje, wówczas asymptota pozioma będzie miała wzór:

Asymptota pozioma - przykład
Należy wyznaczyć asymptotę poziomą funkcji homograficznej y=2-4/(x+3)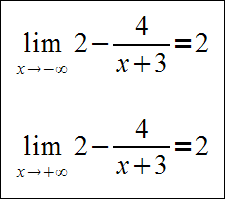
Asymptota pozioma funkcji homograficznej ma wzór y=2.

Asymptoty funkcji - asymptota ukośna
Jeśli istnieją skończone granice funkcji f(x):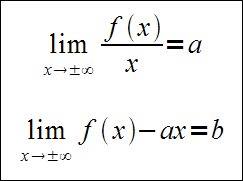
to asymptota ukośna funkcji f(x) ma wzór:

Asymptota ukośna - przykład
Należy wyznaczyć asymptotę ukośną funkcji f(x)=x+1/x.Wyznaczamy granicę (współczynnik a):

Wyznaczamy granicę (współczynnik b):
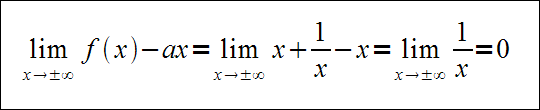
Równanie asymptoty ukośnej będzie miało postać: y=x.

Zobacz artykuły, które mogą Cię zainteresować:
Dodaj komentarz do artykułu.
Komentarze użytkowników (3)
2012-11-29 15:43:46 napisał(a):
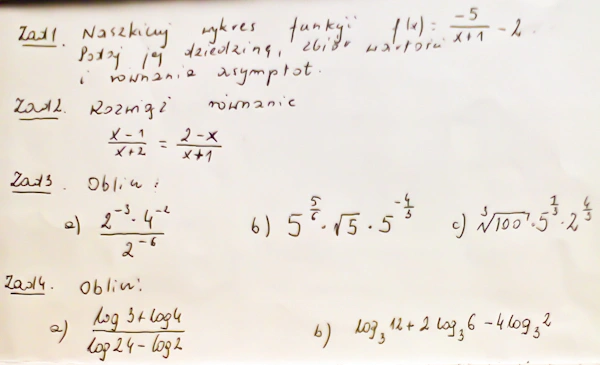
2012-11-29 23:32:11 BazyWiedzy.COM napisał(a):
Witaj.
Oto rozwiązanie zadania nr 2:
W pierwszej kolejności zakładamy, że x jest różne od -2 oraz od -1 (dlatego, że liczby te zerują mianowniki ułamków).
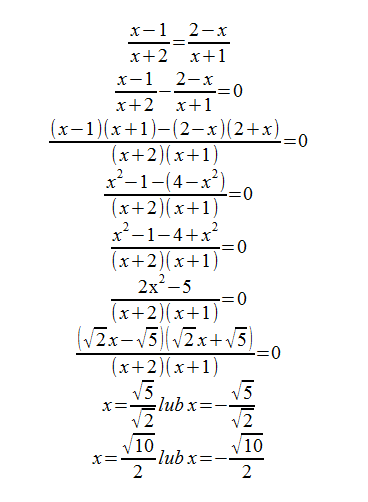
2012-12-01 18:11:13 BazyWiedzy.COM napisał(a):
Oto rozwiązanie zadania 3.
